Question

Out of 100 students 50 fail in English and 30 in Maths. If 12 students fail in both English and Maths, then the number of students passing both the subjects is
(a) 26
(b) 28
(c) 30
(d) 32

Answer 1

Hint: At first take down all the data given and represent it in the form of a Venn diagram then find what is asked in the question.

Complete step-by-step answer:

In the question we are told that out of 100 students 50 fail in English and 30 fail in Maths, now if 12 students fail in both subjects English and Maths, then we have to find the number of students who passed in both subjects.
So, let’s represent number of students who failed in English as n(E), number of students who failed in Maths as n(M) and number of students who failed in both subjects as $n\left( E\cap M \right)$
So, we can write it as,
$\begin{align}
  & n\left( E \right)=50 \\
 & n\left( M \right)=30 \\
 & n\left( E\cap M \right)=12 \\
\end{align}$
So, we can say that n (E only) means students who failed only in English
So, n(E only) = 50 – 12 = 38
Also for maths we can say that n(M only) means students who only failed in Maths.
So, n(M only) = 30 – 12 = 18
Now we can represent it as in in Venn diagram,

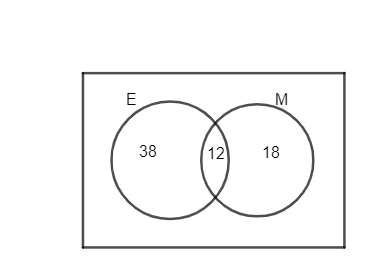
Hence the total number of students who failed is n(E only) + $n(E\cap M)$ + n(M only) which is equal to 38 + 12 + 18 which is 68.
Total students which were given was 100.So the remaining students are 100 – 68 = 32 which have passed in both subject
Hence the correct option is (d).

Note: Students generally get confused between A and only A, B and only B, C and only C. Actually, A means people can read only or A and B or A and C or A and B and C. The same goes for B and C also.