Question

One side open cylinder drum has an inner radius of 28cm and height 2.1m. How much water can be stored in the drum? Express in liters. (1litre\[ = 1000\]cc)

Answer 1

Hint: Here we will find the volume of the cylinder using the given radius and height, and using the volume we will find its storage and express it in liters.

Formula used:
If \[r\]be the radius of a cylinder and \[h\] be the height of the cylinder then its volume is \[V = \pi {r^2}h\]

Complete step by step solution:
The shape of the drum is represented in the diagram below:

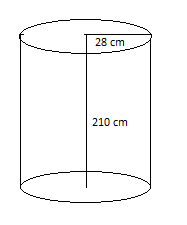
It is given that the radius of the cylinder is \[28\]cm.
The height of the cylinder is \[2.1\]m
Here we are going to multiply the given height by 100 so that the height in meter is converted to height in cm which would be useful in expressing the result in liters.
\[2.1\]m \[ = 210\]cm
We have to find the amount of water that can be stored in the drum.
To find the amount of water initially, we have to find the volume of the drum.
We know that, if \[r\]be the radius of a cylinder and \[h\] be the height of the cylinder then its volume is \[V = \pi {r^2}h\]
Substitute the value of the radius and height in the general form of the volume of the cylinder we have,
\[V = \dfrac{{22}}{7} \times {28^2} \times 210c{m^3}\]
\[V = \dfrac{{22}}{7} \times 28 \times 28 \times 210c{m^3}\]
On simplifying the above equation we get,
\[V = 517440c{m^3}\]
Now we will convert the capacity into liter.
We know that,
1litre\[ = 1000\]cc
So, the amount of water in the drum \[ = \dfrac{{517440}}{{1000}} = 5174.4\]litres

Hence, \[5174.4\]litres of water can be stored in the drum.

Note:
It is given that the shape of the drum is a one-sided cylinder that is nothing but the cylinder which has an opening in the top and closed in the bottom. Even though this is one-sided the volume of the cylinder remains the same that is why we have not changed the formula of the cylinder.