
One mapping is selected at random from all the mappings of the set A=1, 2, 3, ....,n into itself. The probability that the mapping selected is one to one, is given by
a. $\dfrac{1}{{{n^n}}}$
b. $\dfrac{1}{{n!}}$
c. $\dfrac{{(n - 1)!}}{{{n^{n - 1}}}}$
d. None of these.
Answer
589.2k+ views
Hint: Here in this question you need to know two concepts one is probability and other is one to one mapping.
Probability: -
Probability=Favourable outcomes/Total number of outcomes.
Probability can never be greater than one.
One to one mapping: -
One to one or (1-1) function is a relation that preserves the “uniqueness”. Every unique member of the function’s domain is mapped to the unique member of the function’s range. This mapping is sometimes also called as injective mapping.
Complete step-by-step answer: Here given set is A=1, 2, 3, ...., n
Number of ways first element of set A can be mapped = n
Number of ways second element of set A can be mapped = n
Number of ways the third element of set A can be mapped = n and so on.
Total number of mapping from set A to itself=$n \times n \times ...... \times n = {n^n}$ (it is being multiplied to n times)
For one to one mapping: -
Number of ways to map first element in set A=n
Number of ways to map second element in set A=n-1
Number of ways to map third element in set A=n-2
Number of ways to map nth element in set A=1
Total number of one to one mapping from set A to itself=\[n \times (n - 1) \times (n - 2)..... \times 1 = n!\]
$\therefore $ Required probability=Total number of one to one mapping from set A to itself/Total number of mapping from set A to itself
\[ \Rightarrow \dfrac{{n!}}{{{n^n}}} = \dfrac{{n(n - 1)!}}{{{n^n}}}\] (Opening factorial using formula$n! = n(n - 1)(n - 2)(n - 3) \times ....... \times 3 \times 2 \times 1$ )
\[\therefore \dfrac{{(n - 1)!}}{{{n^{n - 1}}}}\] (Using identity $\dfrac{{{x^a}}}{{{x^b}}} = {x^{a - b}}$ )
Hence option C is correct.
Note: Most of the times students got confused in one to one mapping so here is some easy way to understand it using this diagram.
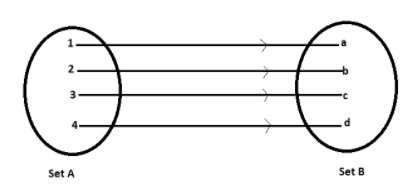
Probability: -
Probability=Favourable outcomes/Total number of outcomes.
Probability can never be greater than one.
One to one mapping: -
One to one or (1-1) function is a relation that preserves the “uniqueness”. Every unique member of the function’s domain is mapped to the unique member of the function’s range. This mapping is sometimes also called as injective mapping.
Complete step-by-step answer: Here given set is A=1, 2, 3, ...., n
Number of ways first element of set A can be mapped = n
Number of ways second element of set A can be mapped = n
Number of ways the third element of set A can be mapped = n and so on.
Total number of mapping from set A to itself=$n \times n \times ...... \times n = {n^n}$ (it is being multiplied to n times)
For one to one mapping: -
Number of ways to map first element in set A=n
Number of ways to map second element in set A=n-1
Number of ways to map third element in set A=n-2
Number of ways to map nth element in set A=1
Total number of one to one mapping from set A to itself=\[n \times (n - 1) \times (n - 2)..... \times 1 = n!\]
$\therefore $ Required probability=Total number of one to one mapping from set A to itself/Total number of mapping from set A to itself
\[ \Rightarrow \dfrac{{n!}}{{{n^n}}} = \dfrac{{n(n - 1)!}}{{{n^n}}}\] (Opening factorial using formula$n! = n(n - 1)(n - 2)(n - 3) \times ....... \times 3 \times 2 \times 1$ )
\[\therefore \dfrac{{(n - 1)!}}{{{n^{n - 1}}}}\] (Using identity $\dfrac{{{x^a}}}{{{x^b}}} = {x^{a - b}}$ )
Hence option C is correct.
Note: Most of the times students got confused in one to one mapping so here is some easy way to understand it using this diagram.

Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

The computer jargonwwww stands for Aworld wide web class 12 physics CBSE

State the principle of an ac generator and explain class 12 physics CBSE




