Question

One kind of cake requires 200 gm of flour and 25 gm of fat, and another kind of cake requires 100 gm of flour and 50 gm of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no shortage of other ingredients used to make the cakes.

Answer 1

Hint: For solving this LPP (Linear programming problem) we will proceed stepwise first we try to do the formulation of the given data into variables and then determine the objective function and then frame the constraints. Then, try to solve for the correct answer.

Complete step-by-step answer:
Given:
One kind of cake requires 200 gm of flour and 25 gm of fat, and another kind of cake requires 100 gm of flour and 50 gm of fat.

Formulation:
Now, let $x$ be the number of cakes which requires 200 gm of flour and 25 gm of fat and $y$ be the number of cakes which requires 100 gm of flour and 25 gm of fat.
Then, our total consumption of flour will be $\left( 200x+100y \right)$ gm and total consumption of fat will be $\left( 25x+50y \right)$ gm for making the total $\left( x+y \right)$ number of cakes.
Objective function $\left( Z \right)$ :
Total number of cakes $=Z=x+y$ .
We have to maximise the value of our objective function.

Constraints:
Now, it is given that we have a total of 5 kg or 5000 gm of flour and we have calculated that our total consumption of flour will be $\left( 200x+100y \right)$ gm. Then, $\left( 200x+100y \right)\le 5000$ or $2x+y\le 50$ is our first constraint equation.
Now, it is given that we have a total of 1 kg or 1000 gm of fat and we have calculated that our total consumption of fat will be $\left( 25x+50y \right)$ gm. Then, $\left( 25x+50y \right)\le 1000$ or $x+2y\le 40$ will be another constraint equation. Moreover, two constraints will be there and they are $x\ge 0$ and $y\ge 0$ .
Finally, we have the following constraints:
$\begin{align}
  & 2x+y\le 50 \\
 & x+2y\le 40 \\
 & x\ge 0,y\ge 0 \\
\end{align}$
Now, we will plot these constraint equations on a graph. The plot is shown below:

Above graph is plotted as per the constraints written above. From the plot, we conclude that the feasible region is OBAC (bounded), and it has four corner points O (0,0) and B (0,20) and A (20,10) and C (25,0). Point B is the intersection of $x+2y=40$ and $y-axis$ . Point A is the intersection of $x+2y=40$ and $2x+y=50$ . Point C is the intersection of $2x+y=50$ and $x-axis$ .
Now, we will calculate the value of our objective function at each corner point. It is shown in the table below:

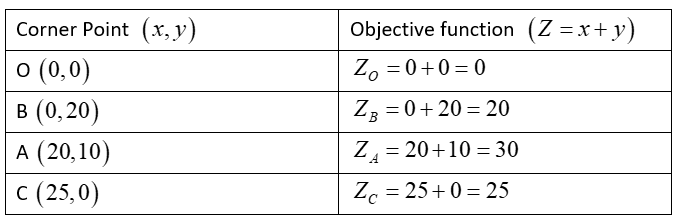
Now, we get the maximum value of our objective function at point A (20,10). But since it is the case of the bounded region, so point A (20,10) is the required point.
Thus, the maximum value of the objective function will be at point A (20,10).
Hence, to make the maximum number of cakes we should make 20 cakes which require 200 gm of flour and 25 gm of fat and 10 cakes which require 100 gm of flour and 50 gm of fat. Total we will make 30 numbers of cakes.

Note: Here, the student should first understand the problem and then proceed stepwise from formulation to the generation of objective function. Then, constraints should be framed accordingly as per the given data. Then, plot the curve carefully and as here the region is bounded so, the corner point at which the value of the objective function will be maximum is our desired point.