Question

On squared paper draw the triangle with vertices at (1,1), (5,3), (3,5). Find the area of the triangle.

Answer 1

Hint: For this question, we need to draw the given points of vertices of a triangle and find out the area of the triangle. Use the formula of the area of a triangle as given below.

Formula used: Area of Triangle $ = \dfrac{1}{2}\left| {\left. {\left( {\begin{array}{*{20}{c}}
  {({x_1} - {x_2}}&{{x_1} - {x_3}} \\
  {{y_1} - {y_2}}&{{y_1} - {y_3}}
\end{array}} \right)} \right|} \right|$ --(1)
where, these vertical lines in equation 1 will represent determinants, and $({x_1},{y_1})$,\[({x_2},{y_2})\],$({x_3},{y_3})$ will represent the coordinates for the vertices of a triangle and more specifically ${x_1},{x_2},{x_3}$ be the x-axis coordinates and ${y_1},{y_2},{y_3}$be the y-axis coordinates.
Now to solve the determinants please use the concept given by equation (2)
\[ = \;\;\left| {\left( {\begin{array}{*{20}{c}}
  a&b \\
  c&d
\end{array}} \right)} \right| = ad - bc\] --(2)
A solution of equation 2 we will get by simple cross-multiplication of opposite diagonal elements and separate them with a negative sign.

Complete step-by-step answer:
(Step 1) Here we will write down the given coordinates and assign it as A=$(1,1), $B=$(3,5), $C= $(5,3)$
(Step 2) Now we will simply plot the coordinates on the x and y-axis with.

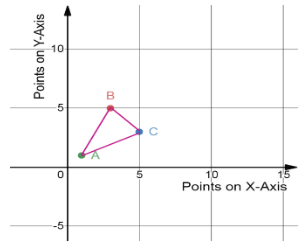
(Step 3) Now simply substitute all the points A, B, and C in equation 1, as discussed in the hint section above.
$ \Rightarrow Area = \dfrac{1}{2}\left| {\left( {\begin{array}{*{20}{c}}
  {(1 - 5)}&{(1 - 3)} \\
  {(1 - 3)}&{(1 - 5)}
\end{array}} \right)} \right|$
(Step 4) Solve the given question with valid points.
$ \Rightarrow Area = \dfrac{1}{2}\left| {\left( {\begin{array}{*{20}{c}}
  { - 4}&{ - 2} \\
  { - 2}&{ - 4}
\end{array}} \right)} \right|$
$ \Rightarrow Area = \dfrac{1}{2}\left| {( - 4)( - 4) - ( - 2)( - 2)} \right|$
$
   \Rightarrow Area = \dfrac{1}{2}\left| {16 - 4} \right| \\
   \Rightarrow Area = \dfrac{1}{2}\left| {12} \right| \\
  \therefore Area = 6unit{s^2} \\
 $
The area of a triangle found from the given coordinates of vertices is \[6\]${(units)^2}$. Remember area is measured in square units but as no dimensions, for now, is mentioned in the question so we have simply represented it as $unit{s^2}$.

Area of the triangle is \[6\]${(units)^2}$

Note: Another approach to solving this question is to make use of the graphical analysis as done on the plotted figure above. Area of any quantity cannot be negative.