Question

On a cold winter day, the atmospheric temperature is $-\theta$ (on Celsius scale) which is below $0^{\circ} C$. A cylindrical drum of height h made of a bad conductor is completely filled with water at $0^{\circ}C$ and is kept outside without any lid. Calculate the time taken for the whole mass of water to freeze.

Answer 1

Hint: Use Fourier’s law of thermal conduction to arrive at an expression for the heat lost by water to the surroundings to form ice. Plug in this expression in the latent heat expression for the fusion of water to form ice. Rearrange this expression in terms of elementary time and evaluate the resultant over the entire height of the cylinder to arrive at the appropriate time that the whole mass of water takes to freeze over.

Formula Used:
Fourier’s thermal conduction law: $\dfrac{Q}{dt} = -KA\dfrac{d\theta}{dx}$
Latent heat: $L=\dfrac{dQ}{dm}$

Complete answer:
When the drum is kept outside without any lid in sub-zero temperatures, i.e., below the freezing point of water, it slowly starts to freeze over by forming ice.

From Fourier’s law of thermal conduction which states that the rate at which heat is transferred between two regions is proportional to the negative of the temperature gradient, i.e.,
$Q \propto -\dfrac{d\theta}{dx} \Rightarrow Q = -K\dfrac{d\theta}{dx}$
Where K is the thermal conductivity.

An integral and differential treatment over time of the above expression results in the solution:
$\dfrac{Q}{dt} = KA\dfrac{d\theta}{dx}$

From which we have the expression for thermal conductivity K as:
$K = \dfrac{Q}{Ad\theta}\dfrac{dx}{dt} $

Let the ice start forming at time t=0, and let x be the thickness of the ice formed. Ice is formed by water losing some amount of heat to the atmosphere. This amount of heat that the water loses in a time interval $t+dt$ is given by:
$dQ = \dfrac{KA\theta}{x}dt$, where K is the thermal conductivity.

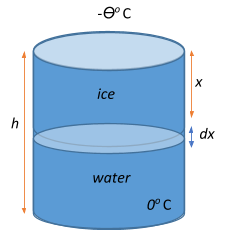
Now, we know that specific latent heat or the latent heat of fusion (L) is a measure of the amount of heat energy $dQ$ per unit mass released or absorbed during a phase change (from water to ice) and denotes the enthalpy change of any amount of substance when it changes phase, i.e.,
$L=\dfrac{dQ}{dm}$

The mass of ice that is formed due to water losing this amount of heat can be given as:
$dm = \dfrac{dQ}{L} = \dfrac{\dfrac{KA\theta}{x}dt}{L} = \dfrac{KA\theta}{xL}dt$

If $ \rho$ is the density of ice over an elementary volume $dv = Adx$ where A is the surface area, the thickness dx of ice is formed in time dt can be given as
$\rho = \dfrac{dm}{dv} = \dfrac{dm}{Adx}$
$\Rightarrow dx = \dfrac{dm}{A\rho} = \dfrac{KA\theta}{xLA\rho}dt == \dfrac{K\theta}{xL\rho}dt $

The time taken for dx amount of ice to freeze:
$\Rightarrow dt = \dfrac{\rho L}{K\theta}xdx$

Therefore, the time taken for all the water to freeze can be calculated by integrating the above expression over the entire height of the cylinder.
${}^t_0\int dt = {}^h_0\int \dfrac{\rho L}{K\theta}xdx $
$\Rightarrow t = \dfrac{\rho L}{K\theta}{}^h_0\int xdx $
$\Rightarrow t = \dfrac{\rho L}{K\theta}\left|\dfrac{x^2}{2}\right|^h_0 =\dfrac{\rho L}{K\theta}.\dfrac{h^2}{2}$
$\Rightarrow t = \dfrac{\rho Lh^2}{2K\theta}$

Note:
Do not get confused between the different types of latent heat. The latent heat of fusion is defined as the amount of heat that must be removed from a unit mass of a substance to change its state from a liquid to a solid, whereas the latent heat of vaporization is the amount of heat that must be added to a unit mass of a substance to change its state from a liquid to a gas, and the latent heat of sublimation is the amount of heat that must be added per unit mass of a substance to change its state from a solid to a gas. Note that all these phase changes are a constant-temperature process.