Question

Obtain the expression for the fringe width in the case of the interference of the light waves.

Answer 1

Hint: To obtain the expression for the fringe width in the case of the interference of the light waves, first we need to construct a figure taking two slits, light emerging from these two slits meets at a point. Distance between screen and slit must be greater than distance between two slits. This way, two triangles will be formed. So apply Pythagoras theorem in both triangles. Calculate distance for each length and then put the values. Subtract these two equations and get the values for the path difference. Then take the path difference for the nth and (n-1) and take the differences, this way we will get fringe width for the interference of the light.

Complete answer:
1. Let ‘s ‘is the source of the monochromatic light of the wavelength d.
2. Let ${{s}_{1}}$ and ${{s}_{2}}$ be the two coherent sources obtained by splitting of the wave front.
3. A screen XY is kept at the distance D from the slits such that D>>d.
4. Draw ${{s}_{1}}$ m and ${{s}_{2}}$ n $\bot $ on XY
5. O is perpendicular bisector of the slit$\therefore {{s}_{1}}o={{s}_{2}}o$, the path difference between the waves reaching at o from ${{s}_{1}}$ and ${{s}_{2}}$ is zero. Therefore O appears as a bright point and ii is the center of the interference pattern known as the central bright point.
6. Suppose D be any point on the screen at a distance of X from central point O.
7. The path difference between the waves reaching at P is ${{s}_{2}}p-{{s}_{1}}p.$

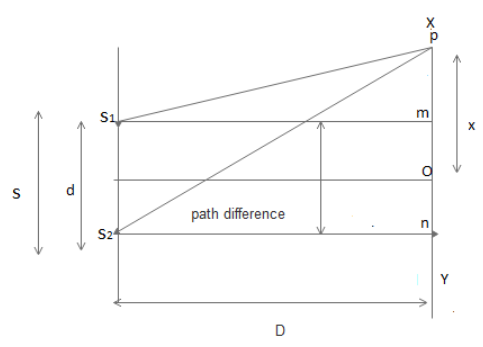
$pm=\left( x-\dfrac{d}{2} \right)$ And $pn=x+\dfrac{d}{2}$
In $\Delta {{s}_{2}}p{{n}_{,}}{{\left( {{s}_{2}}p \right)}^{2}}={{({{s}_{2}}n)}^{2}}+{{(pn)}^{2}}$ . This equation has been written by using Pythagoras theorem.
${{\left( {{s}_{2}}p \right)}^{2}}={{D}^{2}}+{{\left( x+\dfrac{d}{2} \right)}^{2}}$
In $\Delta {{s}_{1}}pm,$
$\begin{align}
  & {{\left( {{s}_{1}}D \right)}^{2}}={{\left( {{s}_{1}}m \right)}^{2}}+{{\left( pm \right)}^{2}} \\
 & ={{D}^{2}}+{{\left( X-\dfrac{d}{2} \right)}^{2}} \\
\end{align}$
Therefore,
$\begin{align}
  & {{\left( {{s}_{2}}p \right)}^{2}}-{{\left( {{s}_{1}}p \right)}^{2}}={{D}^{2}}+{{\left( X+\dfrac{d}{2} \right)}^{2}}-{{D}^{2}}-{{\left( X-\dfrac{d}{2} \right)}^{2}} \\
 & \left( {{s}_{2}}p+{{s}_{1}}p \right)\left( {{s}_{2}}p-{{s}_{1}}p \right)=\left( {{X}^{2}}+Xd+\dfrac{{{d}^{2}}}{4} \right)-\left( {{X}^{2}}-Xd+\dfrac{{{d}^{2}}}{4} \right) \\
\end{align}$
$\begin{align}
  & (({{s}_{2}}p)+({{s}_{1}}p))({{s}_{2}}p-{{s}_{1}}p) \\
 & ={{X}^{2}}+Xd+\dfrac{{{d}^{2}}}{4}-{{X}^{2}}+Xd-\dfrac{{{d}^{2}}}{4} \\
 & \therefore ({{s}_{2}}p-{{s}_{1}}p)=\dfrac{2Xd}{{{s}_{2}}p+{{s}_{1}}p} \\
\end{align}$
Since, X <<< D,
$\begin{align}
  & \therefore {{s}_{2}}p\approx {{s}_{1}}p\approx D \\
 & \therefore {{s}_{2}}p+{{s}_{1}}p\approx 2D \\
\end{align}$
Therefore, ${{s}_{2}}p-{{s}_{1}}p=\dfrac{2Xd}{2D}=\dfrac{Xd}{D}$
This equation gives a path difference between two ways arriving at D.
For constructive interference,
$\begin{align}
  & \Delta X=nd \\
 & \therefore \dfrac{Xd}{D}=nd \\
 & =Y=\dfrac{ndD}{d} \\
\end{align}$
We know that the distance between the center of the two adjacent right or the dark bands is called fringe width or the band width. And it is given by,
Fringe width ($\beta $ ) = ${{X}_{n}}-{{X}_{n-1}}$
$\begin{align}
  & \therefore \beta =\dfrac{ndD}{d}-\left( n-1 \right)\dfrac{dD}{d} \\
 & =\beta =\dfrac{dD}{d} \\
\end{align}$
Hence, fringe width in the case of interference of the light waves.

Note:
The distance between two consecutive dark bands and two consecutive bright bands is $\dfrac{dD}{d}$.thus, distance between consecutive dark bands and the bright bands are equal i.e. bands width of dark and bright bands is the same. Hence, it proves the fringes are equally spaced.