
Observe the following pattern of overlapping triangles made with matchsticks and complete the table. Also, write the general rule that gives the number of matchsticks
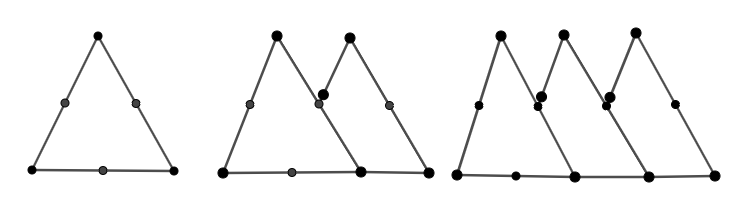
Number of triangles 1 2 3 4 5 6 …. …. Number of matchsticks 6 10 14 …. …. …. …. ….

| Number of triangles | 1 | 2 | 3 | 4 | 5 | 6 | …. | …. |
| Number of matchsticks | 6 | 10 | 14 | …. | …. | …. | …. | …. |
Answer
587.7k+ views
Hint: From the table, you can see that the number of triangles is in A.P. and the number of matchsticks is also in A.P. The number of triangles has a common difference as 1 and number of matchsticks has a common difference of 4. Now, in the question, we have to predict the numbers of matchsticks that are needed when 4 triangles are overlapped which is calculated by adding 4 to the number of matchsticks when 3 triangles are overlapped. Similarly, you can find the number of matchsticks for 5 and 6 number of triangles also. The general rule which gives the number of matchsticks is the ${{n}^{th}}$ term of an A.P. of the matchsticks.
Complete step by step answer:
In the above question, we have given three types of triangles which are constructed by using matchsticks as follows:
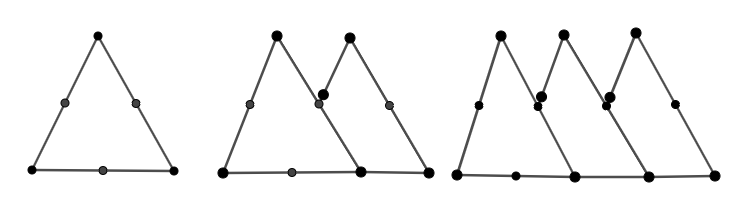
And we are asked to fill the following table and also give the general rule for the relationship between the number of triangles and the matchsticks.
As you can see, the number of matchsticks corresponding to different numbers of triangles is in A.P. The first term (a) of this A.P. is 6 and common difference (d) is equal to 4. Common difference is calculated by subtracting any term from its successor term. Let us pick a term 10 and the successor of this term is 14 so the difference between them is:
$14-10=4$
This is how; we got the common difference as 4.
Now, to get the number of matchsticks corresponding to 4 triangles we are going to add 4 to 14 so the number of matchsticks corresponding to 4 triangles is equal to:
$14+4=18$
Similarly, to get the number of matchsticks corresponding to 5 triangles we are going to add 4 to 18.
$18+4=22$
Now, to get the number of matchsticks corresponding to 6 triangles we are going to add 4 to 22.
$22+4=26$
We are also asked to find the general rule that gives the number of matchsticks which is equal to the ${{n}^{th}}$ term of an A.P.
We know that ${{n}^{th}}$ term of an A.P. is equal to:
\[{{T}_{n}}=a+\left( n-1 \right)d\]
Substituting “a” as 6 and “d” as 4 in the above equation we get,
\[\begin{align}
& {{T}_{n}}=6+\left( n-1 \right)4 \\
& \Rightarrow {{T}_{n}}=6+4n-4 \\
& \Rightarrow {{T}_{n}}=2+4n \\
\end{align}\]
In the above formula, “n” represents the number of triangles.
Note: We can check the number of matchsticks that we have written for 4, 5 and 6 triangles by substituting the value of “n” as 4, 5 and 6 in the general rule that we have found above.
The general rule that we have found above is equal to:
\[{{T}_{n}}=2+4n\]
To get the number of matchsticks for 4 triangles, we are going to substitute the value of n as 4 in the above equation.
\[\begin{align}
& {{T}_{4}}=2+4\left( 4 \right) \\
& \Rightarrow {{T}_{4}}=2+16=18 \\
\end{align}\]
As you can see, the number of matchsticks for 4 triangles which we are getting from the above rule is the same as what we have calculated. This means that we have written the correct number of matchsticks corresponding to 4 triangles.
Similarly, you can check for 5 and 6 triangles and then verify your answer.
Complete step by step answer:
In the above question, we have given three types of triangles which are constructed by using matchsticks as follows:

And we are asked to fill the following table and also give the general rule for the relationship between the number of triangles and the matchsticks.
| Number of triangles | 1 | 2 | 3 | 4 | 5 | 6 | …. | …. |
| Number of matchsticks | 6 | 10 | 14 | …. | …. | …. | …. | …. |
As you can see, the number of matchsticks corresponding to different numbers of triangles is in A.P. The first term (a) of this A.P. is 6 and common difference (d) is equal to 4. Common difference is calculated by subtracting any term from its successor term. Let us pick a term 10 and the successor of this term is 14 so the difference between them is:
$14-10=4$
This is how; we got the common difference as 4.
Now, to get the number of matchsticks corresponding to 4 triangles we are going to add 4 to 14 so the number of matchsticks corresponding to 4 triangles is equal to:
$14+4=18$
| Number of triangles | 1 | 2 | 3 | 4 | 5 | 6 | …. | …. |
| Number of matchsticks | 6 | 10 | 14 | 18 | …. | …. | …. | …. |
Similarly, to get the number of matchsticks corresponding to 5 triangles we are going to add 4 to 18.
$18+4=22$
| Number of triangles | 1 | 2 | 3 | 4 | 5 | 6 | …. | …. |
| Number of matchsticks | 6 | 10 | 14 | 18 | 22 | …. | …. | …. |
Now, to get the number of matchsticks corresponding to 6 triangles we are going to add 4 to 22.
$22+4=26$
| Number of triangles | 1 | 2 | 3 | 4 | 5 | 6 | …. | …. |
| Number of matchsticks | 6 | 10 | 14 | 18 | 22 | 26 | …. | …. |
We are also asked to find the general rule that gives the number of matchsticks which is equal to the ${{n}^{th}}$ term of an A.P.
We know that ${{n}^{th}}$ term of an A.P. is equal to:
\[{{T}_{n}}=a+\left( n-1 \right)d\]
Substituting “a” as 6 and “d” as 4 in the above equation we get,
\[\begin{align}
& {{T}_{n}}=6+\left( n-1 \right)4 \\
& \Rightarrow {{T}_{n}}=6+4n-4 \\
& \Rightarrow {{T}_{n}}=2+4n \\
\end{align}\]
In the above formula, “n” represents the number of triangles.
Note: We can check the number of matchsticks that we have written for 4, 5 and 6 triangles by substituting the value of “n” as 4, 5 and 6 in the general rule that we have found above.
The general rule that we have found above is equal to:
\[{{T}_{n}}=2+4n\]
To get the number of matchsticks for 4 triangles, we are going to substitute the value of n as 4 in the above equation.
\[\begin{align}
& {{T}_{4}}=2+4\left( 4 \right) \\
& \Rightarrow {{T}_{4}}=2+16=18 \\
\end{align}\]
As you can see, the number of matchsticks for 4 triangles which we are getting from the above rule is the same as what we have calculated. This means that we have written the correct number of matchsticks corresponding to 4 triangles.
Similarly, you can check for 5 and 6 triangles and then verify your answer.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Who is eligible for RTE class 9 social science CBSE

What is the Full Form of ISI and RAW

How do you find the valency of chlorine sulphur and class 9 chemistry CBSE

What are the major achievements of the UNO class 9 social science CBSE

Explain the importance of pH in everyday life class 9 chemistry CBSE

Differentiate between parenchyma collenchyma and sclerenchyma class 9 biology CBSE




