Question

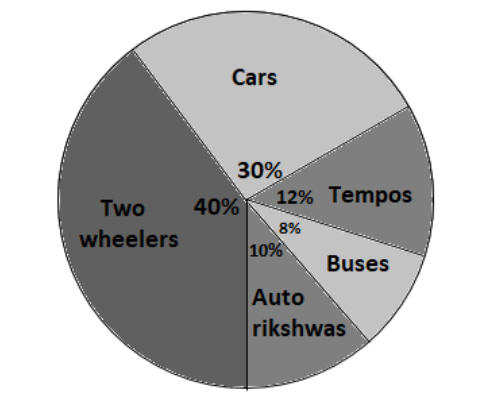
Observe the adjacent pie diagram. It shows the percentages of the number of vehicles passing a signal in a town between 8am and 10am.
I.Find the central angle for each type of vehicle.
II.If the number of two wheelers is 1200, find the number of all vehicles.

Answer 1

Hint: The Central angle of a circle is an angle whose vertex is the center of the circle and the two sides are the radii intersecting the circle at two different points. Using the central angle formula and the data given in the pie chart we will calculate the central angle of each portion. Using the number of two-wheelers given and the central angle for the two- wheeler portion we will find the total number of vehicles.

Complete step by step solution:
The percentage of cars passing a signal is \[30\% \], it means that for a total number of $100$ vehicles $30$ were cars.
The formula for central angle is given by,
\[central\,angle = \dfrac{{Number\,of\,particular\,vehicle}}{{Total\,numbers\,of\,vehicles}} \times {360^ \circ }\]
Therefore, Central angle for Cars $ = \dfrac{{30}}{{100}} \times 360 = {108^ \circ }$
Given the percentage of Tempos is \[12\% \], it means that out of \[100\] vehicles \[12\] were tempos.
$ \Rightarrow $Central angle for Tempos $ = \dfrac{{12}}{{100}} \times 360 = {43.2^ \circ }$
Given the percentage for Buses is \[8\% \], it means out of \[100\] vehicles \[8\] were buses.
\[ \Rightarrow \]Central angle for Buses $ = \dfrac{8}{{100}} \times 360 = {28.8^ \circ }$
Given the percentage for Auto rickshaws is \[10\% \], it means out of \[100\] vehicles \[10\] were Auto rickshaws.
$ \Rightarrow $Central angle for Auto rickshaws $ = \dfrac{{10}}{{100}} \times 360 = {36^ \circ }$
Given the percentage for two wheelers is \[40\% \], it means out of \[100\] vehicles \[40\] were Two wheelers.
$ \Rightarrow $Central angle for two wheelers $ = \dfrac{{40}}{{100}} \times 360 = {144^ \circ }$
Next to find the total number of vehicles, given the number of two wheelers is 1200 also we found the central angle for two wheelers using the above same formula, we will find the total number of vehicles. i.e.
\[central\,angle\,of\,two\,wheeler = \dfrac{{Number\,of\,two\,wheelers}}{{Total\,numbers\,of\,vehicles}} \times {360^ \circ }\]
\[ \Rightarrow \,\,\,Total\,numbers\,of\,vehicles = \dfrac{{Number\,of\,two\,wheelers}}{{Central\,angle\,of\,two\,wheeler}} \times {360^ \circ }\]
$ \Rightarrow $Total number of vehicles $ = \dfrac{{1200}}{{{{144}^ \circ }}} \times {360^ \circ } = 3000$
Therefore, there are a total of 3000 vehicles passing a signal in a town.

Note: If we add all the calculated central angles, we should get their sum as ${360^ \circ }$, as the total angle of a circle is ${360^ \circ }$. In this question the sum of all the central angles is ${108^ \circ } + {43.2^ \circ } + {28.8^ \circ } + {36^ \circ } + {144^ \circ } = {360^ \circ }$. This method can be used to verify our calculation of central angles.