Question

Number of unit cells in $4g$ of $X$(atomic mass $ = 40$), which crystallises in the bcc pattern is: (${N_A}$ is Avogadro’s number)
A. $0.1{N_A}$
B. $2 \times 0.1{N_A}$
C. $\dfrac{{0.1 \times {N_A}}}{2}$
D. $2 \times {N_A}$

Answer 1

Hint: In BCC lattice, the atoms are present at each corner and at the centre of the cubic crystal. For the given question, first find the number of atoms in the given mass of $X$ and the number of atoms comprises one unit cell of the bcc lattice. Then by comparing values, we will get the number of unit cells for a given mass of $X$.

Complete answer:
As we know, for BCC lattice, the atoms are present at each corner and at the centre of the cubic crystal as shown in the figure below:

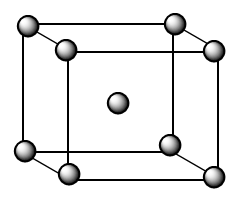
The contribution of each atom present at the corner $ = \dfrac{1}{8}$
The contribution of the atom present at the centre $ = 1$
Therefore, the number of atoms which comprises one unit cell of bcc lattice $ = 8 \times \dfrac{1}{8} + 1 \Rightarrow 2$
Now as per question, the given mass of $X = 4g$
Atomic mass of $X = 40g$
So, the number of moles of $X = \dfrac{{{\text{given mass}}}}{{{\text{atomic mass}}}}$
$ \Rightarrow n = \dfrac{4}{{40}}$
$ \Rightarrow n = 0.1$
Therefore, the number of atoms of $X = n \times {N_A} \Rightarrow 0.1 \times {N_A}$
For BCC unit lattice:
$\because $ 2 atoms comprise to form $ \Rightarrow $1 unit cell
$\therefore 0.1 \times {N_A}$ atoms will comprise to form $ \Rightarrow \dfrac{{0.1 \times {N_A}}}{2}$ unit cells.
Hence for a bcc unit lattice, the number of unit cells in $4g$ of $X$ is $\dfrac{{0.1 \times {N_A}}}{2}$.
So, option (C) is the correct answer.

Note:
Remember that atoms in BCC unit lattice are much more efficiently packed as compared to simple cubic structure, occupying about $68\% $ of the total volume. The coordination number i.e., the number of nearest neighbour atoms in a bcc lattice is eight.