Question

Now ABC is a right-angled triangle in which $\angle A={{90}^{\circ }}$ and AB = AC. Show that $\angle B=\angle C$.

Answer 1

Hint: First let us draw the figure of the triangle with the given condition. Now to the figure let us construct AD such that AD is the angle bisector of the angle A. Now consider the triangle CAD and triangle BAD. In this triangle, we have a common side and AB = AC is given. Since AD is an angle bisector we also have that the angle CAD is equal to the angle BAD. Hence we can easily prove the two triangles congruent by the SAS test of congruence. Now we know that congruent parts of congruent triangles are equal. Using this we will prove the required result.

Complete step-by-step solution:
Let us first consider the triangle ABC such that $\angle A={{90}^{\circ }}$ AB = AC.

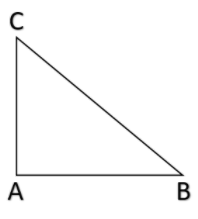
Now let us draw an angle bisector of A. let the bisector meet BC at point D. Hence we get the figure as,

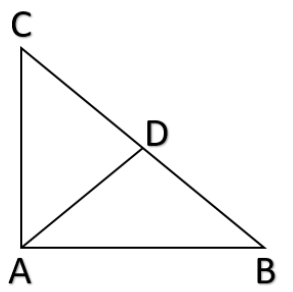
Now note that since AD is an angle bisector we have $\angle BAD=\angle CAD.....................\left( 1 \right)$
Now consider triangles CAD and triangle BAD.
In these triangles we have,
AB = AC
From equation (1) we have
$\angle BAD=\angle CAD$
And since AD is the common side we can say AD = AD.
Hence by SAS test of congruence, we have $\Delta ABD\cong \Delta ACD$
Now we know that congruent parts of congruent triangles are equal hence we get,
$\angle B=\angle C$
Hence we get if AB = AC then $\angle B=\angle C$.

Note: Now note that the result is true for any triangle and not just right-angle triangles. Hence for any triangle, if two sides are equal then the angles opposite to the two sides are also equal. In fact, for any triangle, we can prove this in a similar manner.