Question

How many more different chains can you make using a , a and a ?

Answer 1

Hint: Here the given question is based on the concept of permutation. Here we have to find the possible ways in which the given three shapes can be ordered or arranged in chains. Since it is an arrangement, we use permutation concepts and we determine the solution for the question.

Complete answer: In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements. The word "permutation" also refers to the act or process of changing the linear order of an ordered set.
The formula for permutation of n objects for r selection of objects is given by: \[\,\,{\,^n}{P_r} = \dfrac{{n!}}{{\left( {n - r} \right)!}}\]

Now consider the question, given the three different type of shapes like e , , , and . We have to find several possible ways in which a three-shapes can be ordered or arranged in chains.
We have a three-shapes taken all three at a time then the possible ways of arrangement is \[^3{P_3}\] or simply \[3!\].
Then by the permutation problem
\[ \Rightarrow \,\,{\,^3}{P_3} = \dfrac{{3!}}{{\left( {3 - 3} \right)!}}\]
\[ \Rightarrow \,\,{\,^3}{P_3} = \dfrac{{3!}}{{\left( 0 \right)!}}\]
The value of \[0! = 1\], then
\[ \Rightarrow \,\,{\,^3}{P_3} = \dfrac{{3!}}{1}\]
\[ \Rightarrow \,\,{\,^3}{P_3} = 3!\]
\[ \Rightarrow \,\,{\,^3}{P_3} = 3!\]
\[ \Rightarrow \,\,\,3! = 3 \times 2 \times 1\]
\[\therefore \,\,6\,\,ways\]
The possible ways are shown below:

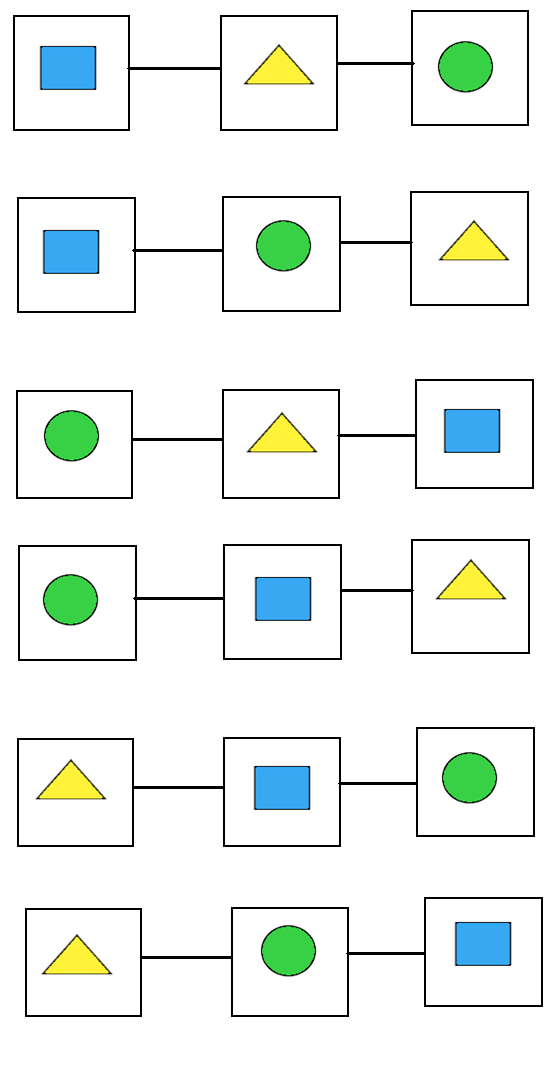
Therefore, in 6 ways the given three shapes can be arranged in different chains.

Note:
Permutation is used when we are counting without replacement and the order matters. If the order does not matter then we can use combinations and the use of the permutation method can easily find out the possible arrangement without doing it manually. Remember, factorial is the continued product of first ‘n’ natural numbers is called the “n factorial” and it is represented by \[n! = \left( {n - 1} \right) \cdot \left( {n - 2} \right) \cdot \left( {n - 3} \right).....3 \cdot 2 \cdot 1\].