
Moment of momentum is called:
A. Torque
B. Impulse
C. Couple
D. Angular momentum
Answer
571.8k+ views
Hint: Momentum of a body is the product of mass and velocity of a body. Now in case of circular motion the moment of momentum comes into play. We will see how the moment of force is defined and from that we will come to the conclusion about what moment of momentum should be called.
Formula used:
\[\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F},\overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p}\]
Complete answer:
Let’s say a body rotates about an axis as shown in the diagram
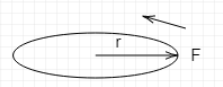
When a body rotates about an axis in a circular path due to the application of a force $F$ which is at a distance$r$ from the axis then the moment of that force about that axis is defined as the
$\tau =r\times F$ . In vector form it is defined as \[\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F},\] and is called the torque.
So in case of rotational motion we get a moment of any quantity by multiplying it with the distance from the axis. Now If a particle of linear momentum $p$ rotates about an axis in a circular path of radius $r$ as shown in the diagram
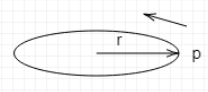
Then its angular momentum is defined as
\[L=r\times p\] and in vector form it is given by
\[\overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p}\]. Thus we see that we get the angular momentum of a body by multiplying its linear momentum with distance from the rotating axis. Thus like incase of force we can say the angular momentum is the moment of momentum.
So the correct option is D.
Note:
Any two quantities which are the same should have the same dimensions. If we compare the dimensions of the given quantities then we will see that only angular momentum and moment of momentum will have the same dimensions. But this question is an analytical one so we should explain it with the analogy of moment of force.
Formula used:
\[\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F},\overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p}\]
Complete answer:
Let’s say a body rotates about an axis as shown in the diagram

When a body rotates about an axis in a circular path due to the application of a force $F$ which is at a distance$r$ from the axis then the moment of that force about that axis is defined as the
$\tau =r\times F$ . In vector form it is defined as \[\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F},\] and is called the torque.
So in case of rotational motion we get a moment of any quantity by multiplying it with the distance from the axis. Now If a particle of linear momentum $p$ rotates about an axis in a circular path of radius $r$ as shown in the diagram
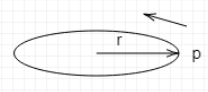
Then its angular momentum is defined as
\[L=r\times p\] and in vector form it is given by
\[\overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p}\]. Thus we see that we get the angular momentum of a body by multiplying its linear momentum with distance from the rotating axis. Thus like incase of force we can say the angular momentum is the moment of momentum.
So the correct option is D.
Note:
Any two quantities which are the same should have the same dimensions. If we compare the dimensions of the given quantities then we will see that only angular momentum and moment of momentum will have the same dimensions. But this question is an analytical one so we should explain it with the analogy of moment of force.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




