Question

What is the mirror formula? Derive the relation $\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{2}{R}$ for a concave mirror?

Answer 1

Hint: First of all draw the ray diagram. Consider the required right triangles and compare their side length as well as the angles. The focal length of the mirror is double that of the radius of curvature of the mirror. And also the sign convention should be taken care of well. This will help you in answering this question.

Complete step by step solution:

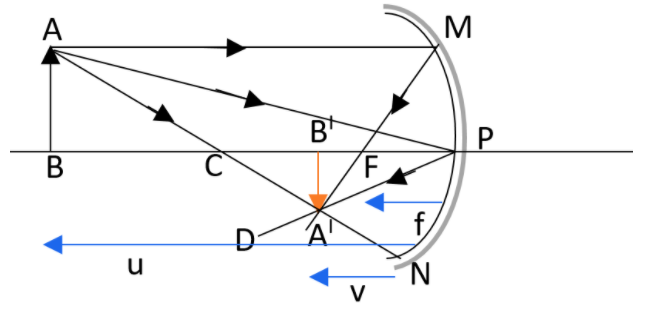
The mirror formula is the formula which shows the relation between the focal length, image distance and object distance of a mirror. The diagram is representing the ray diagram of a concave mirror considering three rays. It shows the image ${A}'{B}'$ of an object $AB$ created by a concave mirror which is real in this case. Therefore, point ${A}'$is the point of image $A$ when every ray initializes at point $A$ and the incident on the concave mirror after a reflection passes through the point ${A}'$. From the diagram, the two right-angled triangles ${A}'{B}'F$ and $MPF$ are identical. That is for paraxial rays, $MP$can be taken to be a straight line
perpendicular to $CP$. Hence,
$\begin{align}
  & \dfrac{{B}'{A}'}{PM}=\dfrac{{B}'F}{FP} \\
 & or \\
 & \dfrac{{B}'{A}'}{BA}=\dfrac{{B}'F}{FP} \\
\end{align}$………. (1)
As the angles $\angle APB=\angle {A}'{P}'{B}'$, the right triangles ${A}'{B}'P$ and $ABP$ are similar.
Therefore we can write that,
\[\dfrac{{B}'{A}'}{BA}=\dfrac{{B}'P}{BP}\]…… (2)
Let us compare equations (1) and (2),
\[\dfrac{{B}'F}{FP}=\dfrac{{B}'P-FP}{FP}=\dfrac{{B}'P}{BP}\] ………… (3)
Equation (3) is basically a relation which consists of magnitudes of distances. Let us now apply the sign convention. We can see that light is travelling from the body to
the mirror\[MPN\]. Therefore this can be taken as the positive direction. In order to reach the object\[AB\], the image \[{A}'{B}'\] and also the focus \[F\] from the pole\[P\], we have to move in the opposite direction of incident light. Thus all the three will be having negative signs. That is,
\[\begin{align}
  & {B}'P=-v \\
 & FP=-f \\
 & BP=-u \\
\end{align}\]
Let us use these conventions in the equation (3). That is,
\[\begin{align}
  & \dfrac{-v+f}{-f}=\dfrac{-v}{-u} \\
 & \Rightarrow \dfrac{v-f}{f}=\dfrac{v}{u} \\
\end{align}\]
As we all know the focal length is twice the radius of curvature.
\[f=\dfrac{R}{2}\]
Therefore from this the mirror equation has been obtained as
$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{2}{R}$
Hence the answer has been calculated.

Note:
The focal length of the mirror or lens is defined as the point at which an image is formed by the rays from the infinity incident on the mirror. All the parameters will be negative if the direction is opposite to that of the incident light. This is the sign convention.