Question

An ideal diatomic gas undergoes a thermodynamic process as shown in the PV diagram. The heat input during the process a to b is?

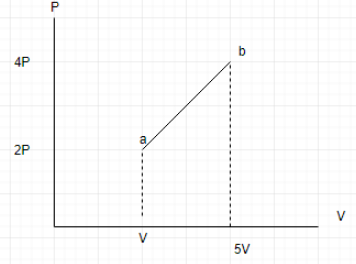
Answer 1

Hint:This is PV diagram and we know that the area under PV diagram gives us the work done. So, we can use the first law of thermodynamics which gives a relationship between the heat input to the system and the increase in the internal energy of the system and the work done. In order to find out the change in the internal energy we need to find the temperatures at point a and b by using the ideal gas law.

Complete step by step answer:
In order to find the area, we divide the area under the curve as the sum of triangle and rectangle. The area under the curve gives us the work done on the system.

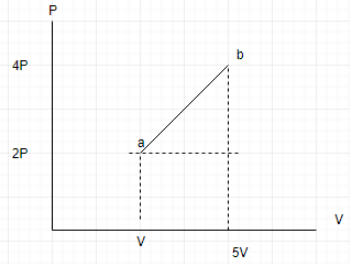
Required area= \[\dfrac{4V\times 2P}{2}+4V\times 2P\]
\[\Delta W=12VP\]
Also, we use ideal gas law at points a and b.
From ideal gas law, assuming number of moles to be 1,
$PV=nRT \\
\Rightarrow 2Pv=R{{T}_{a}} \\
\therefore {{T}_{a}}=\dfrac{2PV}{R} \\$
At point b:
$PV=nRT \\
\Rightarrow 20PV=R{{T}_{b}} \\
\therefore {{T}_{a}}=\dfrac{20PV}{R} \\$
Now change in temperature,
$\Delta T={{T}_{b}}-{{T}_{a}} \\
\Rightarrow \Delta T= \dfrac{20PV}{R}-\dfrac{2PV}{R} \\
\therefore \Delta T=\dfrac{18PV}{R} \\$
Now for diatomic has change in internal energy is given by:
$\Delta U=\dfrac{5}{2}R\Delta T \\
\Rightarrow \Delta U=\dfrac{5}{2}R\times \dfrac{18PV}{R} \\
\therefore \Delta U=45PV \\ $
Now we can use the first law of thermodynamics, \[\Delta Q=\Delta U+\Delta W\], putting the values we get,
$\Delta Q=45PV+12PV \\
\therefore\Delta Q=57 PV $

Hence, the heat input during the process a to b is $57PV$.

Note:We have used ideal gas law here because it was mentioned in the question that the gas is ideal. Otherwise we would have to use real gas laws. Here the work done on the system comes out to be positive, if the case would have been opposite that work is done by the system then the work would have been taken in negative. So, we have to be careful in using sign conventions.