Question

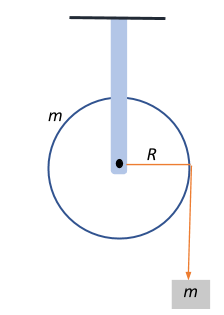
A mass $m$ is supported by a massless string wound around a uniform hollow cylinder of mass $m$ and radius $R$. If the string does not slip on the cylinder, with what acceleration will the mass fall on release?

A. $\dfrac{5g}{6}$
B. $g$
C. $\dfrac{2g}{3}$
D. $\dfrac{g}{2}$

Answer 1

Hint: A good starting point would be to establish two different expressions for the tension in the string. In other words, obtain an expression for tension in the string in the context of the suspended mass and then obtain a second tension expression keeping the string-cylinder picture in mind. Equate the two since the tension in the string is the same everywhere at a given point in time, and you should arrive at a suitable expression for the body’s acceleration when released. Remember to also account for rotational acceleration and torque that essentially produce linear acceleration.

Formula Used:
Linear (tangential) acceleration $a = R\alpha$, where R is the radius of motion and $\alpha$ is the angular acceleration.
Torque in rotational kinematics: $\tau = I\alpha$ where I is the rotational inertia (moment of inertia) and $\alpha$ is the angular acceleration.

Complete step by step answer:
Let us deconstruct the setup into two parts to understand the influencing parameters that produce motion.
Let us first look at mass $m$ that is suspended from the massless string.
We are given that the string does not slip on the cylinder, which means that the suspended body will never undergo freefall and will always have an acceleration that exists in addition to the one due to gravity. Let this acceleration be $a$.
This linear acceleration $a$ arises tangentially from the angular acceleration $\alpha$ of the string sliding along the rim of the cylinder. Therefore, we have $a = R\alpha$

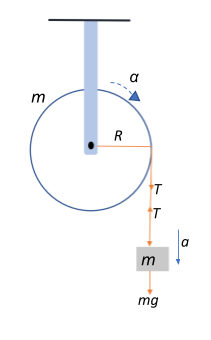
Now, the since the body is suspended, the weight of the body produces a tension $T$ in the string, which balances out the weight and the acceleration of the body, i.e.,
$T = mg – ma \Rightarrow T= mg – mR\alpha$.
Now let us look at the string-cylinder setup.
The torque produced from the angular movement of the string as a result of its angular acceleration about the cylinder of mass $m$ and radius $R$ can be given as:
$\tau = I \times \alpha $ where I is the rotational inertia given as $I = mR^2$
$\Rightarrow \tau = mR^2\alpha = mR^2\left(\dfrac{a}{R}\right) \Rightarrow \tau = mRa$
This rotational torque produces a linear torque tangentially and is given as
$\tau = T \times R$
Equating the two we get,
$mRa = T \times R \Rightarrow ma = T$
However ,when we looked at the suspended body, we found that $T = mg – ma $
Therefore, we can now find the acceleration of the mass when released by equating the two:
$\Rightarrow ma = mg – ma \Rightarrow 2ma=mg \Rightarrow a=\dfrac{g}{2}$
Therefore the correct option would be D. $\dfrac{g}{2}$

Note:
It is important to understand the relation between the linear(tangential) acceleration $a$ and angular acceleration $\alpha$:
We know that linear acceleration can be expressed as the rate of change of linear velocity $a = \dfrac{\Delta v}{\Delta t}$ where the linear velocity can be expressed as angular velocity as $v = \dfrac{\Delta r \omega}{\Delta t}$ where \omega is the angular velocity.
$\Rightarrow a = r\dfrac{\Delta \omega}{\Delta t}$. Here $\dfrac{\Delta \omega}{\Delta t}$ is nothing but the angular acceleration $\alpha$. Therefore, we get the final relation $a = r\alpha$
It is also useful to distinguish torque in linear and rotational kinematics.
In linear kinematics $\tau = \vec{r} \times \vec{F}$, while in rotational kinematics:
$\tau = I\alpha$ where I is the rotational inertia (moment of inertia) and $\alpha$ is the angular acceleration.