Question

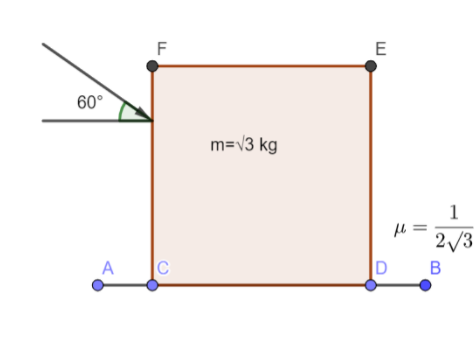
What is the maximum value of force F such that the block shown in the arrangement does not move?

Answer 1

Hint: Friction is a type of force. Whenever a body moves or slides over a surface with non-zero coefficient of friction, it tends to move. This motion is due to the frictional force. The direction of motion is opposite to the frictional force.

There are two types of friction.
Static friction
Kinetic friction
Limiting friction is the maximum value of frictional force such that there is no motion experienced.
Under the equilibrium condition, the body experiences limiting friction and does not undergo motion.

Complete step by step solution:
We will first visualize the forces using a free body diagram of the mass m given in the question.
The free body diagram is given below

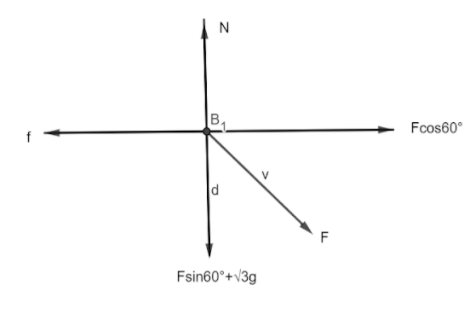
In this diagram, N represents the normal reaction on the block, f represents the limiting friction and F represents the applied force.
The components of the applied force F have been shown.
For vertical equilibrium,
$N = \sqrt 3 g + F\sin {60^0}$ .
For horizontal equilibrium,
$f = F\cos {60^0}$ .
But we know that $f = \mu N$ where $\mu $ is the coefficient of friction.
Substituting the value of N,
$f = \mu (\sqrt 3 g + F\sin {60^0})$
Thus, we have $f = \mu (\sqrt 3 g + F\sin {60^0}) = F\cos {60^0}$
Substituting the appropriate values,
$\dfrac{1}{{2\sqrt 3 }}(\sqrt 3 g + F \times \dfrac{{\sqrt 3 }}{2}) = \dfrac{F}{2}$
Further solving the equation, we get,
$\dfrac{{\sqrt 3 }}{{2\sqrt 3 }}(g + \dfrac{F}{2}) = \dfrac{F}{2}$
$ \Rightarrow \dfrac{1}{2}(10 + \dfrac{F}{2}) = \dfrac{F}{2}$ (Taking g=10 $m\,{s^{ - 2}}$ )
$ \Rightarrow 5 + \dfrac{F}{4} = \dfrac{F}{2}$
Solving this equation we will get,
$ \Rightarrow 5 = \dfrac{{2F - F}}{4}$
$ \Rightarrow F = 20\,N$
So, when the applied force is $F = 20\,N$ , the body will not move.

Note:
We might confuse the value of frictional force to be $f = \mu mg$ . However, this happens only when there is no external applied force and the weight of the body is equal to the normal reaction. In all other cases where the weight is not equal to the normal reaction, we take $f = \mu N$ . This gives the exact value of the frictional force applied and would help to avoid any mistake.