Question

Magnetic field at point O will be

A.\[\dfrac{{{\mu }_{0}}l}{2R}\operatorname{int}erior\]
B.$\dfrac{{{\mu }_{0}}l}{2R}exterior$
C.$\dfrac{{{\mu }_{0}}l}{2R}\left( 1-\dfrac{1}{\pi } \right)\operatorname{int}erior$
D.$\dfrac{{{\mu }_{0}}l}{2R}\left( 1+\dfrac{1}{\pi } \right)exterior$

Answer 1

HintMagnetic field due to a straight wire and magnetic field due to a circular loop are opposite to each other.

 Complete step-by-step solution:
Magnetic field:- The region near a magnet, where a magnetic needle experiences a torque and rests in a definite direction is called magnetic field.
When current flows in a conductor, then a magnetic field is produced around it. Magnetic field lines depend on the shape of the conductor.
For a straight wire
When the current is flow in a straight wire, then magnetic field lines in circular shape around it and the formula for magnetic field in a straight wire is
${{B}_{1}}=\dfrac{{{\mu }_{0}}}{2\pi }\dfrac{i}{R}$
Where ${{B}_{1}}=$ The magnetic field
$i=$ The current in the wire
$R=$ The distance of point O from the wire
Direction of the magnetic field is upward.
For circular loop
When current is flowing in a wire which is circular shape, then the magnetic field lines in circular loop but different way
    

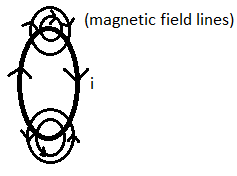
Formula of magnetic field for circle
${{B}_{2}}=\dfrac{{{\mu }_{0}}i}{2R}$
Where $B=$ The magnetic field, $i=$ Current and $R=$ Radius of circle
Direction of the magnetic field is downward.
So the effective magnetic field due to both straight wire and circular loop is
$B={{B}_{1}}={{B}_{2}}$
$B=\dfrac{{{\mu }_{0}}i}{2R}-\dfrac{{{\mu }_{0}}i}{2\pi R}$
$B=\dfrac{{{\mu }_{0}}i}{2R}\left( 1-\dfrac{1}{\pi } \right)$

Note:
When students find out the resultant magnetic field. Students added both, but the magnetic field is a vector quantity so the direction has an important role. Both magnetic fields ${{B}_{1}}$ and ${{B}_{2}}$ are opposite in direction. So subtract these magnetic fields from higher to lower.