Question

M is the foot of the perpendicular from a point P on the parabola ${y^2} = 8\left( {x - 3} \right)$ to its directrix and S is the focus of the parabola. If $\Delta SPM$ is an equilateral triangle, then find the length of each side of the triangle.
(A) $2$
(B) $3$
(C) $4$
(D) $8$

Answer 1

Hint:Try to analyse the given equation and make a figure of a parabola on the coordinate plane. Assume a point lying on parabola as $P\left( {x,y} \right)$ and using these assumptions find coordinates of point M. Use the distance formula $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $ to find the expression for all sides. Equate all three expressions and find values of $x{\text{ and }}y$. Substitute these values to find the length of sides.

Complete step-by-step answer:
Let’s first analyse the given information in the question. Here the equation of a parabola is given as ${y^2} = 8\left( {x - 3} \right)$ . The focus is named as S and from a point P on the curve; a perpendicular is drawn to a directrix named PM. Now we need to find the length of the triangle $\Delta SPM$ , if it is an equilateral triangle.
As we know that, for a general equation of parabola of the form ${\left( {y - k} \right)^2} = 4a\left( {x - h} \right)$, we have:
Focus$ = S\left( {h + a,k} \right)$
Equation of Directrix$:x = h - a$
Vertex$ = \left( {h,k} \right)$
Axis$:y = k$
In our case, we have ${y^2} = 8\left( {x - 3} \right) = 4 \times 2\left( {x - 3} \right)$, with $k = 0,h = 3{\text{ and }}a = 2$ .
Therefore, we get:
Focus$ = \left( {3 + 2,0} \right) = S\left( {5,0} \right)$
Equation of Directrix$:x = 3 - 2 \Rightarrow x = 1$
Vertex$ = \left( {3,0} \right)$
Axis$:y = 0$
With this information, we can now easily draw the diagram of this parabola as shown in the figure below:

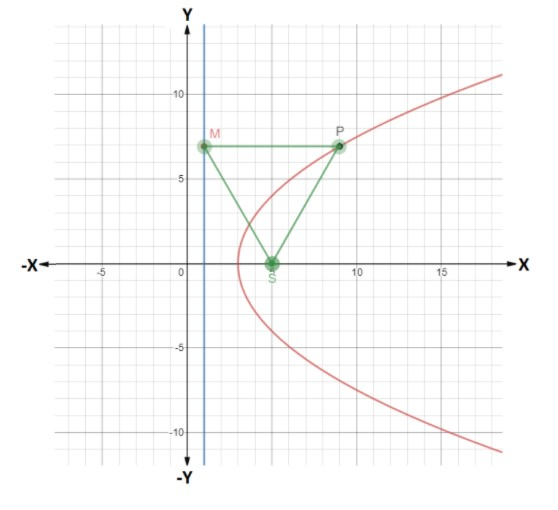
Now, let assume the given point P on the parabola as $P\left( {x,y} \right)$ . The point M lies on the directrix and parallel to point $P\left( {x,y} \right)$ so the coordinates of M will be $\left( {1,y} \right)$ . And the point S is the focus parabola with coordinates $\left( {5,0} \right)$ .
According to the question these points S, P and M are the corners of the equilateral triangle. And for finding the length of sides of $\Delta SPM$ we need to calculate the distance between these points.
We know about distance formula, which says that the two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ , the distance d between these points is given by the formula:
$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
Using the above relation we can write the distance between points $P\left( {x,y} \right)$ and $M\left( {1,y} \right)$ as:
$PM = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y - y} \right)}^2}} = \sqrt {{{\left( {x - 1} \right)}^2} + 0} = \sqrt {{{\left( {x - 1} \right)}^2}} $
Similarly, the distance between $M\left( {1,y} \right)$ and $S\left( {5,0} \right)$ can be calculated as:
$MS = \sqrt {{{\left( {5 - 1} \right)}^2} + {{\left( {0 - y} \right)}^2}} = \sqrt {{4^2} + {y^2}} = \sqrt {16 + {y^2}} $
And for the side joining point $P\left( {x,y} \right)$ and $S\left( {5,0} \right)$ we have:
$SP = \sqrt {{{\left( {x - 5} \right)}^2} + {{\left( {y - 0} \right)}^2}} = \sqrt {{{\left( {x - 5} \right)}^2} + {y^2}} $
But the triangle is equilateral, and thus have all the sides equal to each other:
$ \Rightarrow SP = PM = MS \Rightarrow \sqrt {{{\left( {x - 5} \right)}^2} + {y^2}} = \sqrt {{{\left( {x - 1} \right)}^2}} = \sqrt {16 + {y^2}}.....................(i)$
So, here we got three expressions in variable $x$ and $y$ equal to each other. On squaring all of them, we get:
$ \Rightarrow {\left( {x - 5} \right)^2} + {y^2} = {\left( {x - 1} \right)^2} = 16 + {y^2}.....................(ii)$
Let’s equate first and the last expression from (ii), we get
$ \Rightarrow {\left( {x - 5} \right)^2} + {y^2} = 16 + {y^2}$
Now, this can be solved for the value of $x$ after subtracting ${y^2}$ from both sides.
$ \Rightarrow {\left( {x - 5} \right)^2} = 16$
Taking square root on both sides we get:
$ \Rightarrow x - 5 = \sqrt {16} = \pm 4 \Rightarrow x = \pm 4 + 5 \Rightarrow x = 9{\text{ or }}x = 1$
Since $x = 1$ is the equation of directrix and point P lies on the parabola.
Therefore, we get $x = 9$
Value of $x = 9$ can be substituted in (ii) to find the value of $y$ as:
$ \Rightarrow {\left( {9 - 5} \right)^2} + {y^2} = {\left( {9 - 1} \right)^2} = 16 + {y^2} \Rightarrow 16 + {y^2} = 64$
It can be further solved to find the values of $y$ as:
$ \Rightarrow 16 + {y^2} = 64 \Rightarrow {y^2} = 64 - 16 = 48 \Rightarrow y = \sqrt {48} = \pm 4\sqrt 3 $
Here we get two values of $y = \pm 4\sqrt 3 $ and both of them lie on the parabola and both of these values are correct and satisfies our conditions.
So, we can consider any of the two values for the triangle $\Delta SPM$. Let’s take $y = 4\sqrt 3 $
Therefore, we got the coordinates of the corner points as $P\left( {9,4\sqrt 3 } \right)$ , $M\left( {1,4\sqrt 3 } \right)$ and $S\left( {5,0} \right)$
Using these values in (i), we will get:
$ \Rightarrow SP = PM = MS = \sqrt {{{\left( {9 - 5} \right)}^2} + {{\left( {4\sqrt 3 } \right)}^2}} = \sqrt {{{\left( {9 - 1} \right)}^2}} = \sqrt {16 + {{\left( {4\sqrt 3 } \right)}^2}} = \sqrt {{8^2}} = 8{\text{ units}}$
Thus, we get the length of the side of the triangle $\Delta SPM$ as $8{\text{ units}}$.

So, the correct answer is “Option D”.

Note:Try to draw the diagram using the given information in the question. This will help you visualize better. Be careful while solving the quadratic equation for the values of $x$ and $y$. Remember that a quadratic equation always has two roots, do not drop any root.
An alternative approach for the same problem can be taken by utilizing the measure of angles in the figure. As we know that all interior angles of an equilateral triangle are $60^\circ $ and PM is perpendicular to the directrix. This will give us a right angle triangle with hypotenuse as MS and with angles $30^\circ ,60^\circ {\text{ and }}90^\circ $. We can use trigonometric ratios for finding the length of hypotenuse MS from other sides.