Question

What is the locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line \[4x - 5y = 20\] to the circle \[{x^2} + {y^2} = 9\]?
(a). \[20({x^2} + {y^2}) - 36x + 45y = 0\]
(b). \[20({x^2} + {y^2}) + 36x - 45y = 0\]
(c). \[20({x^2} + {y^2}) - 20x + 45y = 0\]
(d). \[20({x^2} + {y^2}) + 20x - 45y = 0\]

Answer 1

Hint: Determine the tangent and the chord of contact of the tangents from the point (h, k) that lies of the line \[4x - 5y = 20\]. Assume (a, b) to be the midpoint of the chord. Find the relation between a and b, and replace a and b with x and y respectively.

Complete step-by-step answer:

We need to find the locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line \[4x - 5y = 20\] to the circle \[{x^2} + {y^2} = 9\].

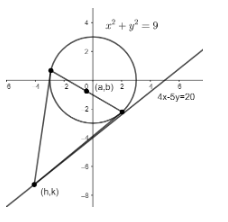
Consider a point (h, k) on the line \[4x - 5y = 20\], then, we have:
\[4h - 5k = 20.............(1)\]
The equation of chord of contact of the tangents to the circle \[{x^2} + {y^2} = 9\] from a point (a, b) outside the circle is given by:
\[ax + by = 9\]
The equations of chord of contact of the tangents from the point (h, k) to the circle \[{x^2} + {y^2} = 9\] is then given as follows:
\[hx + ky = 9..........(2)\]
Let (a, b) be the mid-point of the chord of contact of the tangents.
Then, the equation of the chord with the midpoint (a, b) is given as follows:
\[ax + by = {a^2} + {b^2}..........(3)\]
Line in equation (2) and equation (3) are the same. Hence, we have:
\[\dfrac{h}{a} = \dfrac{k}{b} = \dfrac{9}{{{a^2} + {b^2}}}\]
The value of h in terms of a and b is given by:
\[h = \dfrac{{9a}}{{{a^2} + {b^2}}}..........(4)\]
The value of k in terms of a and b is given by,
\[k = \dfrac{{9b}}{{{a^2} + {b^2}}}..........(5)\]
Substituting equations (4) and (5) in equation (1), we have:
\[4\left( {\dfrac{{9a}}{{{a^2} + {b^2}}}} \right) - 5\left( {\dfrac{{9b}}{{{a^2} + {b^2}}}} \right) = 20\]
Simplifying, we get:
\[36a - 45b = 20({a^2} + {b^2})\]
\[20({a^2} + {b^2}) - 36a + 45b = 0\]
Replacing a and b with x and y respectively, we get:
\[20({x^2} + {y^2}) - 36x + 45y = 0\]
Hence, the correct answer is option (a).

Note: The equation of the chord with a midpoint (a, b) is \[ax + by = {a^2} + {b^2}\]. The equation of the chord of contact of tangents drawn from the point (h, k) outside the circle \[{x^2} + {y^2} = {a^2}\] is \[hx + ky = {a^2}\].