
Locate $ \sqrt 3 $ on the number line.
Answer
568.5k+ views
Hint: We will first plot the $ \sqrt 2 $ to locate $ \sqrt 3 $ on the number line. We can plot $ \sqrt 2 $ on the number line with the help of the Pythagoras theorem. This can be done by finding the values of base and perpendicular to get the hypotenuse is $ \sqrt 2 $ . Now, after this, we will plot this length on the number by drawing an arc. Now with this length $ \sqrt 2 $ we will plot $ \sqrt 3 $ by considering $ \sqrt 2 $ as base and 1 as perpendicular. The length of the hypotenuse is the required length and again, with the help of compass we will locate it on the number line.
Complete step-by-step answer:
To locate $ \sqrt 3 $ on the number line, we will use the Pythagoras theorem.
We know that
$ 1 + 2 = 3 $
Squaring both the sides we will get,
$ {1^2} + {2^2} = {3^2} $
This is in the form of Pythagoras theorem, 1 as perpendicular, $ 2 $ as base and $ 3 $ as hypotenuse.
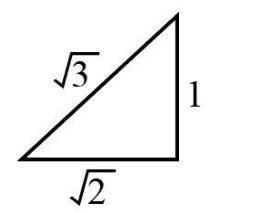
We know that the expression of Pythagoras theorem is
\[\begin{array}{c}
\Rightarrow {\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Bas}}{{\rm{e}}^2} + \Rightarrow {\rm{Perpendicula}}{{\rm{r}}^2}\\
\Rightarrow {\rm{Hypotenuse}} = \sqrt {{\rm{Bas}}{{\rm{e}}^2} + {\rm{Perpendicula}}{{\rm{r}}^2}}
\end{array}\]
We will substitute 1 as perpendicular and $ 2 $ as base in the above expression.
\[\begin{array}{l}
\Rightarrow {\rm{Hypotenuse}} = \sqrt {{2^2} + {1^2}} \\
\Rightarrow {\rm{Hypotenuse}} = \sqrt 3
\end{array}\]
Firstly we will locate $ \sqrt 2 $ on the number line as :
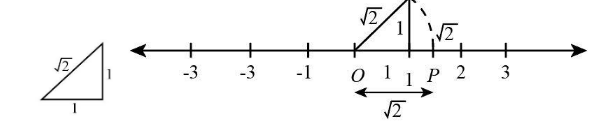
We will locate 1 on the number line then we will draw a perpendicular from the point of magnitude 1 unit. After that, we join the end point of perpendicular to the origin of the number line. The length of the hypotenuse comes out to be $ \sqrt 2 $ .
Now we will draw an arc from the origin and length equal to hypotenuse on the number line.
To locate $ \sqrt 3 $ ,
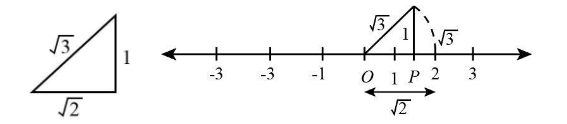
We will draw a perpendicular of magnitude 1 unit from the length $ \sqrt 2 $ . Now we will join the endpoint of perpendicular to the origin of the number line.
Now we will draw an arc from the origin and length equal to hypotenuse on the number line. This is the required length.
Note: In this question, we are locating the roots with the help of Pythagoras theorem. We can represent the number as a hypotenuse of the triangle by finding the respective values of base and perpendicular. We should use a compass carefully to locate the points on the number line.
Complete step-by-step answer:
To locate $ \sqrt 3 $ on the number line, we will use the Pythagoras theorem.
We know that
$ 1 + 2 = 3 $
Squaring both the sides we will get,
$ {1^2} + {2^2} = {3^2} $
This is in the form of Pythagoras theorem, 1 as perpendicular, $ 2 $ as base and $ 3 $ as hypotenuse.
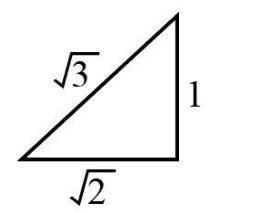
We know that the expression of Pythagoras theorem is
\[\begin{array}{c}
\Rightarrow {\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Bas}}{{\rm{e}}^2} + \Rightarrow {\rm{Perpendicula}}{{\rm{r}}^2}\\
\Rightarrow {\rm{Hypotenuse}} = \sqrt {{\rm{Bas}}{{\rm{e}}^2} + {\rm{Perpendicula}}{{\rm{r}}^2}}
\end{array}\]
We will substitute 1 as perpendicular and $ 2 $ as base in the above expression.
\[\begin{array}{l}
\Rightarrow {\rm{Hypotenuse}} = \sqrt {{2^2} + {1^2}} \\
\Rightarrow {\rm{Hypotenuse}} = \sqrt 3
\end{array}\]
Firstly we will locate $ \sqrt 2 $ on the number line as :

We will locate 1 on the number line then we will draw a perpendicular from the point of magnitude 1 unit. After that, we join the end point of perpendicular to the origin of the number line. The length of the hypotenuse comes out to be $ \sqrt 2 $ .
Now we will draw an arc from the origin and length equal to hypotenuse on the number line.
To locate $ \sqrt 3 $ ,

We will draw a perpendicular of magnitude 1 unit from the length $ \sqrt 2 $ . Now we will join the endpoint of perpendicular to the origin of the number line.
Now we will draw an arc from the origin and length equal to hypotenuse on the number line. This is the required length.
Note: In this question, we are locating the roots with the help of Pythagoras theorem. We can represent the number as a hypotenuse of the triangle by finding the respective values of base and perpendicular. We should use a compass carefully to locate the points on the number line.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

What are gulf countries and why they are called Gulf class 8 social science CBSE





