Question

How many lines of symmetry are there for an isosceles triangle?
A. 1
B. 2
C. 3
D. 0

Answer 1

Hint: First of all, draw the diagram of the isosceles triangle. The line of symmetry is the imaginary line where you could fold the image and have both halves match exactly. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer:
We know that the line of symmetry is the imaginary line where you could fold the image and have both halves match exactly.
If we fold the isosceles triangle vertically, we can find two equal shapes of right-angled triangles. So, the folded line can be treated as a line of symmetry for the isosceles triangle as shown in the figure:

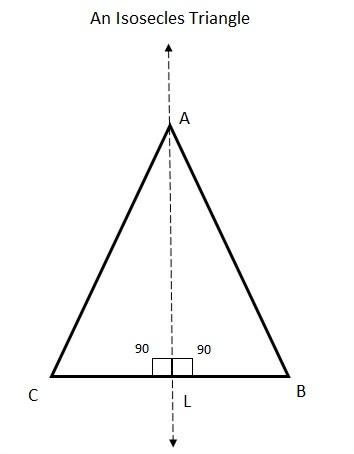
Consider the triangles \[\Delta ACL\] and \[\Delta ABL\]
\[
   \Rightarrow \angle ALC = \angle ALB = {90^0}{\text{ }}\left( {{\text{common right angles}}} \right) \\
   \Rightarrow \angle ACL = \angle ABL{\text{ }}\left( {{\text{Angles of adjacent sides of isosceles triangle are equal}}} \right) \\
\]
Hence by AA congruence rule, \[\Delta ACL \cong \Delta ABL\].
Thus, By the line \[L\] the isosceles triangle is divided into two parts.
As there is no chance for another line of symmetry, it has only one line of symmetry i.e., vertical line of symmetry.
Thus, the correct option is A. 1

Note: The formed two triangles by the line of symmetry are right-angled triangles having the same area. The AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other.