Question

Lines \[{{L}_{1}}:\dfrac{x-6}{3}=\dfrac{y-4}{2}=z-2\] and \[{{L}_{2}}:\dfrac{x-8}{4}=y-2=\dfrac{z-4}{2}\] meets plane \[\pi :\overrightarrow{r}\cdot (2\widehat{i}+\widehat{j}-\widehat{k})=7\]at points \[A,B\] then find area of triangle formed by the lines \[{{L}_{1}},{{L}_{2}}\] and \[AB\] is :
A). \[\dfrac{7}{2}\sqrt{\dfrac{19}{2}}\]
B). \[\sqrt{\dfrac{19}{2}}\]
C). \[\dfrac{\sqrt{11}}{4}\]
D). \[6\sqrt{5}\]

Answer 1

Hint: First of all assume the point of intersection of both the lines be \[\lambda \] and \[\mu \]after that find out the value of \[\lambda \] and \[\mu \] by equating the equations, then find out the value of plane of line by applying vector dot product and we can find out the point of intersection of \[A\] and \[B\] then find out the area of triangle and check which option is correct in the above given options.

Complete step-by-step solution:
We have given two lines:
\[\Rightarrow {{L}_{1}}:\dfrac{x-6}{3}=\dfrac{y-4}{2}=z-2\] mark it as equation \[(1)\]
\[\Rightarrow {{L}_{2}}:\dfrac{x-8}{4}=y-2=\dfrac{z-4}{2}\] mark it as equation \[(2)\]
Let the point of intersection for equation \[(1)\]be \[\lambda \]
Now according to equation \[(1)\] we will find out the values of \[x,y,z\]
\[\Rightarrow \dfrac{x-6}{3}=\lambda \]
\[\Rightarrow x-6=3\lambda \]
\[\Rightarrow x=3\lambda +6\] mark it as equation \[(3)\]
Similarly find out the value of \[y\]
\[\Rightarrow \dfrac{y-4}{2}=\lambda \]
\[\Rightarrow y-4=2\lambda \]
\[\Rightarrow y=2\lambda +4\] mark it as equation \[(4)\]
Now find the value of \[z\]
\[\Rightarrow z-2=\lambda \]
\[\Rightarrow z=\lambda +2\] mark it as equation \[(5)\]
Let the point of intersection for equation \[(2)\]be \[\mu \]
Now according to equation \[(2)\] we will find out the values of \[x,y,z\]
\[\Rightarrow \dfrac{x-8}{4}=\mu \]
\[\Rightarrow x-8=4\mu \]
\[\Rightarrow x=4\mu +8\] mark it as equation \[(6)\]
Similarly find out the value of \[y\]
\[\Rightarrow y-2=\mu \]
\[\Rightarrow y=\mu +2\] mark it as equation \[(7)\]
Now find the value of \[z\]
\[\Rightarrow \dfrac{z-4}{2}=\mu \]
\[\Rightarrow z-4=2\mu \]
\[\Rightarrow z=2\mu +4\] mark it as equation \[(8)\]
Equating the equation \[(3)\] and \[(6)\] we get:
\[\Rightarrow 3\lambda +6=4\mu +8\]
\[\Rightarrow 3\lambda -4\mu =8-6\]
\[\Rightarrow 3\lambda -4\mu =2\] mark it as equation \[(9)\]
Equating the equation \[(4)\] and \[(7)\] we get:
\[\Rightarrow 2\lambda +4=\mu +2\]
\[\Rightarrow 2\lambda -\mu =2-4\]
\[\Rightarrow 2\lambda -\mu =-2\] mark it as equation \[(10)\]
Now to find the value of \[\lambda \] we will multiply equation \[(10)\] by \[4\] on both sides, then subtract it from equation \[(9)\] we will get:
\[\Rightarrow \left( 2\lambda -\mu \right)\times 4=-2\times 4\]
\[\Rightarrow 8\lambda -4\mu =-8\]
Now subtract equation \[(9)\] from it:
\[\Rightarrow 8\lambda -4\mu -\left( 3\lambda -4\mu \right)=-8-2\]
\[\Rightarrow 8\lambda -4\mu -3\lambda +4\mu =-10\]
\[\Rightarrow 5\lambda =-10\]
\[\Rightarrow \lambda =-\dfrac{10}{5}\]
\[\Rightarrow \lambda =-2\]
Hence the point of intersection will be \[C(0,0,0)\]
We have given \[\pi :\overrightarrow{r}\cdot (2\widehat{i}+\widehat{j}-\widehat{k})=7\]
As we know that \[\overrightarrow{r}=x\widehat{i}+y\widehat{j}+z\widehat{k}\] , put the value of \[\overrightarrow{r}\] we get:
\[\Rightarrow x\widehat{i}+y\widehat{j}+z\widehat{k}\cdot (2\widehat{i}+\widehat{j}-\widehat{k})=7\]
Apply dot product:
\[\Rightarrow 2x+y-z=7\]
We will find the intersection point for \[{{L}_{1}}\] by putting the values of \[x,y,z\] from equation \[(3),(4),(5)\]
\[\Rightarrow 2x+y-z=7\]
\[\Rightarrow 2\left( 3\lambda +6 \right)+2\lambda +4-\left( \lambda +2 \right)=7\]
\[\Rightarrow 6\lambda +12+2\lambda +4-\lambda -2=7\]
\[\Rightarrow 7\lambda =-7\]
\[\Rightarrow \lambda =-1\]
Point \[A\] will be: \[\left( 3\lambda +6,2\lambda +4,\lambda +2 \right)\]
Put the value of \[\lambda \] we get:
\[\Rightarrow A(3,2,1)\]
We will find the intersection point for \[{{L}_{2}}\] by putting the values of \[x,y,z\] from equation \[(6),(7),(8)\]
\[\Rightarrow 2x+y-z=7\]
\[\Rightarrow 2\left( 4\mu +8 \right)+\mu +2-\left( 2\mu +4 \right)=7\]
\[\Rightarrow 8\mu +16+\mu +2-2\mu -4=7\]
\[\Rightarrow 7\mu =-7\]
\[\Rightarrow \mu =-1\]
Point \[B\] will be: \[\left( 4\mu +8,\mu +2,2\mu +4 \right)\]
Put the value of \[\mu \] we get:
\[\Rightarrow B(4,1,2)\]
Hence to find the area of triangle will be:

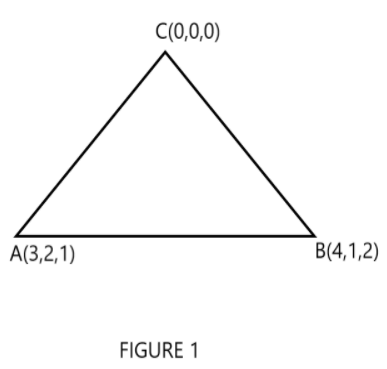
If we write it in vector form then:
\[\Rightarrow \overrightarrow{AC}=3\widehat{i}+2\widehat{j}+\widehat{k}\]
\[\Rightarrow \overrightarrow{BC}=4\widehat{i}+\widehat{j}+2\widehat{k}\]
\[\Rightarrow \text{Area of triangle=}\dfrac{1}{2}\left| \overrightarrow{AC}\times \overrightarrow{BC} \right|\]
Now we will find the value of \[\overrightarrow{AC}\times \overrightarrow{BC}\]
\[\Rightarrow \overrightarrow{AC}\times \overrightarrow{BC}=\left| \begin{align}
  & \widehat{i}\text{ }\widehat{j}\text{ }\widehat{k} \\
 & 3\text{ }2\text{ }1 \\
 & 4\text{ }1\text{ }2 \\
\end{align} \right|\]
\[=3\widehat{i}-\widehat{j}(2)+\widehat{k}(-5)\]
\[= 3\widehat{i}-2\widehat{j}-5\widehat{k}\]
\[\Rightarrow \left| \overrightarrow{AC}\times \overrightarrow{BC} \right|=\sqrt{9+4+25}\]
\[\Rightarrow \left| \overrightarrow{AC}\times \overrightarrow{BC} \right|=\sqrt{38}\]
Therefore Area of triangle \[ABC\] will be
\[\Rightarrow \dfrac{1}{2}\times \sqrt{38}\]
\[= \dfrac{\sqrt{38}}{2}\]
\[= \dfrac{\sqrt{2}\times \sqrt{19}}{2}\]
\[= \dfrac{\sqrt{2}\times \sqrt{19}}{2}\times \dfrac{\sqrt{2}}{\sqrt{2}}\]
\[= \dfrac{2\times \sqrt{19}}{2\sqrt{2}}\]
\[=\sqrt{\dfrac{19}{2}}\]
Hence option \[(B)\] is correct as the area of the triangle is \[\sqrt{\dfrac{19}{2}}\].

Note: Students you know that the total of a triangle's interior angles is always 180o, regardless of how the triangle is created and no matter how a triangle is made, it can always be broken into two right triangles. Any of a triangle's sides is shorter than the total of the other two sides.