Question

Light ray is incident at an angle 45° on glass sphere. The light ray emerges out parallel to diameter AB as shown. The value of the refractive index of the material is?

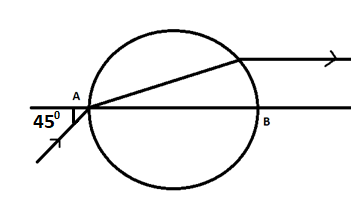
Answer 1

Hint: Angle of incidence is given, as the light is travelling from a rarer (air) to a denser (glass) medium, it will suffer refraction. Angle of refraction can be measured by applying geometry, then from Snell’s law, we can calculate the refractive index of the material.
Snell’s law:
$\dfrac{{\sin i}}{{\sin r}} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$ where, i and r are angle of incidence and refraction respectively.
${\mu _1}$ is refractive index of medium from where light is incident and ${\mu _2}$ is refractive index of medium to where light enters
Refractive index of air is 1.

Complete step by step answer:
The ray of light is entering from air to glass i.e. travels from rarer to denser medium, thus the ray moves away from the normal.

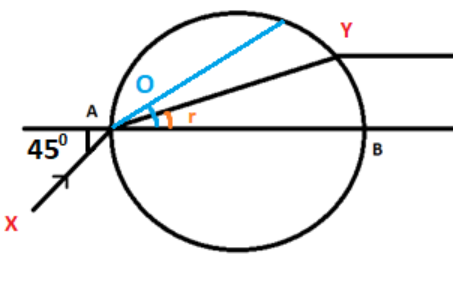
XA is incident and AY is refracted ray
Angle of incidence $\left( {\angle i} \right)$= 45° (given)
Calculating the value for angle of refraction r:
$\angle i = \angle O$ (Vertically opposite angles)
$ \Rightarrow \angle O = {45^o}$
Now the refracted ray is bisecting $\angle O$
$
   \Rightarrow \angle O = 2\angle r \\
   \implies \angle r = \dfrac{{\angle O}}{2} \\
   \implies \angle r = \dfrac{{{{45}^o}}}{2} \\
   \implies \angle r = {22.5^o} \\
$
Now, according to Snell’s law:
$\dfrac{{\sin i}}{{\sin r}} = \dfrac{{{\mu _2}}}{{{\mu _1}}}$
Medium 1 is air because the ray of light is travelling from air, its refractive index is 1, so:
${\mu _1} = 1$
Medium 2 is glass sphere because the ray of light is entering it, we need to calculate its refractive index, so:
${\mu _2} = ?$
Substituting all the values, we get:
$\dfrac{{\sin {{45}^o}}}{{\sin {{22.5}^o}}} = \dfrac{{{\mu _2}}}{1} \\$
$\implies \sin {45^o} \times 1 = \sin {22.5^o} \times {\mu _2} \\$
$\implies 0.70 = 0.38 \times {\mu _2}$ $(\because \sin {45^o} = 0.70 \\$
$\implies \sin {22.5^o}$ = $0.38 \\ $
$\implies {\mu _2}$ = $\dfrac{{0.70}}{{0.38}} \\$
$\implies {\mu _2}$ = $1.84 \\ $
Therefore, refractive index of the material is 1.84
Refractive index has no units.

Note:
The phenomenon happening here is known as refraction of light, this happens due to different speeds of light in different mediums. The medium in which the speed of light is more is known as rarer and in which it is less is known as denser medium.
Refractive index is basically the speed of light in a medium with respect to air. Since we have speeds in both numerator and denominator, their units cancel out and thus the refractive index is unit less.