Question

Light is incident from glass ( $\mu =1.5$ ) to air. Sketch the variation of angle of deviation $\delta $ with the angle of incident $i$ for $0

Answer 1

Hint: Angle of deviation is the difference between angle of incidence and angle of refraction. After a critical angle, the light ray undergoes total internal reflection, so now the angle of deviation Is now the angle between the incident ray and the reflected ray. The sine of critical angle is the inverse of refractive index.

Formulas used:
$\mu =\dfrac{c}{v}=\dfrac{\angle i}{\angle r}$
$\sin C=\dfrac{1}{\mu }$

Complete step-by-step solution:
When light travels from one medium to another, it deviates from its original path. This phenomenon is known as refraction.

The refractive index of a material is calculated as-
$\mu =\dfrac{c}{v}=\dfrac{\angle i}{\angle r}$
Here, $\mu $ is the refractive index
$c$ is the speed of light in air
$v$ is the speed of light in medium
$\angle i$ is the angle of incidence
$\angle r$ is the angle of refraction

When light travels from a denser medium to a rarer medium, for an angle of incidence in the rarer medium the angle of refraction is ${{90}^{o}}$, this angle is known as the critical angle. When the angle of incidence increases more than the critical angle than total internal reflection takes place.

For $\mu =1.5$, the critical angle is-
$\sin C=\dfrac{1}{\mu }$

Here, $C$ is the critical angle. We substitute given values in the above equation to get,
$\begin{align}
  & \sin C=\dfrac{1}{1.5} \\
 & \Rightarrow C={{\sin }^{-1}}\dfrac{10}{15} \\
 & \Rightarrow C={{\sin }^{-1}}\dfrac{2}{3} \\
 & \therefore C={{42}^{o}} \\
\end{align}$

Therefore, the critical angle is ${{42}^{o}}$.

The angle of deviation is the difference between the angle of incidence and the angle of refraction.
$\delta =\left| \angle i-\angle r \right|$
Here, $\delta $ is the angle of deviation.

The angle of deviation varies with angle of incidence as-

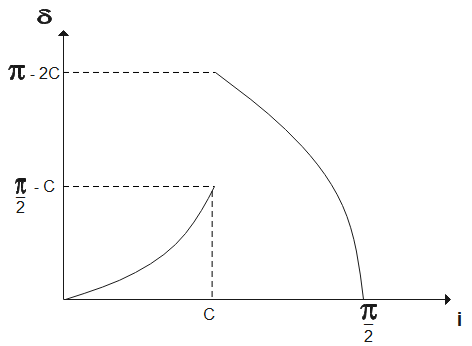
After the incident angle attains critical angle, the light ray undergoes total internal reflection for all angles greater than the critical angle. Also, the angle of deviation increases suddenly upto almost half after incident angle is equal to the critical angle. When-
$\begin{align}
  & \angle i=0 \\
 & \Rightarrow \mu =\dfrac{0}{r} \\
 & \therefore r=0 \\
\end{align}$

When, $\angle i=90$ in reflection, the light ray is along the normal so it will follow the same path along the normal.
$\therefore \angle r=0$

Therefore, the graph between angle of deviation and the angle of incidence shows both refraction and reflection.

Note:
In reflection, the angle of deviation is the angle between the incident ray and the reflected ray. When the angle of incidence is equal to the critical angle, the angle of refraction is the right angle. The refractive index of a material is a constant quantity; it does not have any unit as it is a ratio of two quantities with the same unit.