Question

Let w (Im w \[ \ne 0\]) be a complex number. Then the set of all complex number z satisfying the equation $w - \bar wz = k\left( {1 - z} \right)$ , for some real number k, is:
A) $\left\{ {z:\left| z \right| = 1} \right\}$
B) $\left\{ {z:z = \bar z} \right\}$
C) $\left\{ {z:z \ne 1} \right\}$
D) $\left\{ {z:\left| z \right| = 1,z \ne 1} \right\}$

Answer 1

Hint: A number of the form $\left( {a + ib} \right)$ , where $a{\text{ and }}b$ are real numbers, is called a complex number, $a$ is called the real part, and $b$ called the imaginary part.
Here, $i$ is called iota and equals $\sqrt { - 1} $ .
Imaginary value (or part) (or number) is the value that combines with iota, $i$.
The conjugate of the complex number $z = a + ib$ , denoted by $\bar z$ , is given by $\bar z = a - ib$.
In complex equations, generally $z = x + iy$ is a complex variable.
Roots of a complex equation in a variable $z$, is the value of $z$ which satisfies the complex equation.

Complete step-by-step answer:
Step 1: Substitute complex numbers in the given equation.
Let complex number, $w = a + ib$, provided $b \ne 0$
Thus, its conjugate, $\bar w = a - ib$
$
  w - \bar w = a + ib - \left( {a - ib} \right) \\
   \Rightarrow w - \bar w = a + ib - a + ib = 2ib \\
 $
But given that $b \ne 0$
$\therefore w - \bar w \ne 0$ …… (1)
We know, $z = x + iy$
Given the complex equation: $w - \bar wz = k\left( {1 - z} \right)$
Here, k is a real number.
Substituting the values of $w,\bar w,z$ in given equation.
\[a + ib - \left[ {\left( {a - ib} \right)\left( {x + iy} \right)} \right] = k\left( {1 - \left( {x + iy} \right)} \right)\]

Step 2: Further simplifying the equation:
\[ \Rightarrow a + ib - \left[ {ax + iay - ibx - {i^2}by} \right] = k\left( {1 - x - iy} \right)\]
We know, $i = \sqrt 1 $
Therefore, put ${i^2} = - 1$
\[
   \Rightarrow a + ib - \left[ {ax + iay - ibx + by} \right] = k\left( {1 - x - iy} \right) \\
   \Rightarrow a + ib - ax - iay + ibx - by = k - kx - iky \\
 \]
Combining imaginary terms and real terms:
\[ \Rightarrow a - ax - by + i\left( {b - ay + bx} \right) = \left( {k - kx} \right) - iky\]
When two complex numbers are equal, their respective real parts and imaginary parts are equal. For example:
 $
  s + it = 2 + i(x - 3) \\
   \Rightarrow s = 2;t = \left( {x - 3} \right) \\
 $
Therefore, \[a - ax - by = k - kx\]
    \[
   \Rightarrow a - ax - by = k\left( {1 - x} \right) \\
   \Rightarrow k = \dfrac{{a - ax - by}}{{\left( {1 - x} \right)}} \\
 \] …… (2)
And \[b - ay + bx = - ky\]
\[ \Rightarrow k = \dfrac{{b - ay + bx}}{{ - y}}\] …… (3)
From equation (3) and (4)
\[ \Rightarrow \dfrac{{a - ax - by}}{{\left( {1 - x} \right)}} = \dfrac{{b - ay + bx}}{{ - y}}\]
\[
   \Rightarrow - y\left( {a - ax - by} \right) = \left( {1 - x} \right)\left( {b - ay + bx} \right) \\
   \Rightarrow - ay + axy + b{y^2} = b - bx - ay + axy + bx - b{x^2} \\
   \Rightarrow {\text{ }}b{y^2} = b - b{x^2} \\
   \Rightarrow {\text{ }}b{y^2} + b{x^2} = b \\
   \Rightarrow {\text{ }}{x^2} + {y^2} = 1 \\
 \]
Taking square root on both sides
\[ \Rightarrow {\text{square root on both sides}}\sqrt {{x^2} + {y^2}} = \sqrt 1 = 1\] ...... (4)
The modulus of the complex number $z = x + iy$ , is equal to the square root of the sum of squares of the real part and imaginary part, denoted by $\left| z \right|$ , i.e.,
$\left| z \right| = \sqrt {{x^2} + {y^2}} $
From equation (4)
$\left| z \right| = \sqrt {{x^2} + {y^2}} = 1$
For $z = 1$ , in the given equation
$w - \bar wz = k\left( {1 - z} \right)$
$
   \Rightarrow w - \bar w\left( 1 \right) = k\left( {1 - 1} \right) \\
   \Rightarrow w - \bar w = 0 \\
 $
But this contradicts with the equation (1) i.e. $w - \bar w \ne 0$
Hence, $z \ne 1$
Final answer: Then the set of all complex number z satisfying the equation is $\left| z \right| = 1$ but $z \ne 1$ . Thus, the correct option is (D).
Graphical representation

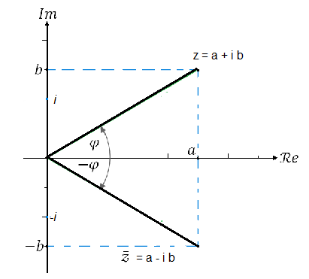
Note: Square of Modulus of a complex number is equal to the product of the number and its conjugate.
i.e. ${\left| z \right|^2} = z \cdot \bar z$
Alternate steps for simplifying the given complex equation:
$
  w - \bar wz = k\left( {1 - z} \right) \\
   \Rightarrow w - \bar wz = k - kz \\
   \Rightarrow w - k = - kz + \bar wz \\
   \Rightarrow w - k = z\left( {\bar w - k} \right) \\
 $
Taking modulus and then squaring both sides.
\[ \Rightarrow {\left| {w - k} \right|^2} = {\left| {z\left( {\bar w - k} \right)} \right|^2}\]
We know, ${\left| z \right|^2} = z \cdot \bar z$
\[ \Rightarrow \left( {w - k} \right)\left( {\overline {w - k} } \right) = {\left| z \right|^2}\left( {\bar w - k} \right)\left( {\overline {\bar w - k} } \right)\]
Given that k is a real number, therefore conjugate of k = k.
\[ \Rightarrow \left( {w - k} \right)\left( {\bar w - k} \right) = {\left| z \right|^2}\left( {\bar w - k} \right)\left( {w - k} \right)\]
\[
   \Rightarrow \left( {w - k} \right)\left( {\bar w - k} \right) - {\left| z \right|^2}\left( {\bar w - k} \right)\left( {w - k} \right) = 0 \\
   \Rightarrow \left[ {\left( {w - k} \right)\left( {\bar w - k} \right)} \right]\left( {1 - {{\left| z \right|}^2}} \right) = 0 \\
 \]
\[
  \left( {1 - {{\left| z \right|}^2}} \right) = 0 \\
   \Rightarrow {\left| z \right|^2} = 1 \\
   \Rightarrow \left| z \right| = 1 \\
 \]
\[
  \left[ {\left( {w - k} \right)\left( {\bar w - k} \right)} \right] = 0 \\
   \Rightarrow \left( {w - k} \right)\left( {\overline {w - k} } \right) = 0 \\
   \Rightarrow {\left| {w - k} \right|^2} = 0 \\
   \Rightarrow w - k = 0 \\
   \Rightarrow w = k \\
 \]
But k is a real number, so w would also be a real number. But it contradicts that the w is a complex number. That’s why $w \ne k$
Form the above solution we have, $z \ne 1$. Hence, the correct option is (D).