Question

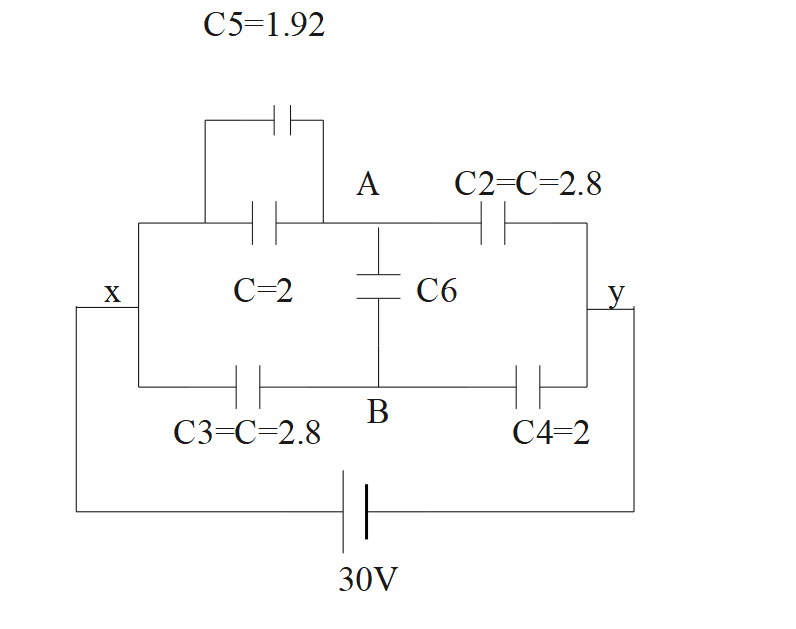
Let us connect two more capacitors in the circuit. One of them, ${{C}_{5}}$​, is connected in the part of the circuit between x and a. It could be either in series or parallel with ${{C}_{1}}$​. The other, ${{C}_{6}}$​, is connected between a and b. It is observed whether we increase ${{C}_{6}}$​ or reduce it, equivalent capacitance between x and y has the same value. Capacitance ${{C}_{5}}$​ :

A) 1.24 in series with $C_1$
B) 1.92 in parallel with $C_1$
C) 2.28 in series with $C_1$
D) 2.56 in parallel with $C_1$

Answer 1

Hint: Let us first find the potential difference across the capacitor 4. Next, let us find the equivalent capacitance across the branch by. Also, we must use the formula of wheatstone bridge in the circuit. Find the values of capacitors 1 and 5, and decide if they’re connected in series or parallel. Finally find the value of capacitor 5.
Formula used:
q=cv

Complete answer:
It is given that if we connect a and b by a wire, then electron will flow from a to b that means b is at higher potential than a
${{V}_{B}}-{{V}_{A}}=5V$
if ${{C}_{1}}$ is at x potential difference then potential at point a will be ${{V}_{A}}=(30-X)V$
and point b will be at $\begin{align}
  & {{V}_{B}}=30-(30-X) \\
 & \Rightarrow {{V}_{B}}=XV \\
\end{align}$
now,
 $\begin{align}
  & {{V}_{B}}-{{V}_{A}}=5V \\
 & \Rightarrow X-(30-X)=5V \\
 & \Rightarrow X=17.5V \\
\end{align}$
Potential difference across ${{C}_{4}}=17.5V$
$\begin{align}
  & {{V}_{4}}={{V}_{1}} \\
 & {{V}_{4}}=17.5V \\
\end{align}$

Consider any branch, say xay.
Since ${{C}_{1}},{{C}_{2}}$​ are in series, charge on ${{C}_{2}}$ is equal to charge on ${{C}_{1}}$
${{Q}_{2}}={{Q}_{1}}=32\mu C$
Using q+cv for ${{C}_{2}}$
${{C}_{2}}=C=\dfrac{35}{{{V}_{2}}}=2.8\mu C$
Equivalent capacitance of branch xay is the series equivalent of
$\begin{align}
  & {{C}_{1}}=2\mu F,{{C}_{2}}=2.8\mu F \\
 & {{C}_{NET}}=1.17\mu F \\
\end{align}$
I.e.,
Equivalent capacitance of branch xby is the series equivalent of
${{C}_{3}}=2.8\mu F$and $\begin{align}
  & {{C}_{4}}=2\mu F \\
 & {{C}_{EQ}}=1.17\mu F \\
\end{align}$. These branches are in parallel between x and y. Hence, equivalent capacitance between x and y is
$1.17+1.17\mu F=2.34\mu F$
Capacitor ${{C}_{5}}$ is connected in the part of circuit between x and a either in series or parallel with ${{C}_{1}}=2\mu F$.let the equivalent capacitance of ${{C}_{1}},{{C}_{5}}$ ​i.e., the equivalent capacitance between x and a be ${{C}_{1}}^{1}$
Capacitor ${{C}_{6}}$​ is connected between a and b. Obviously, the circuit then becomes a Wheatstone bridge. Further, since equivalent capacitance between x and y is independent of the value of ${{C}_{6}}$​, it implies that the bridge is in the balanced condition and potentials at a and b are now equal, so that
$\begin{align}
  & \dfrac{{{C}_{1}}^{1}}{{{C}_{3}}}=\dfrac{{{C}_{2}}}{{{C}_{4}}} \\
 & {{C}_{1}}=3.92\mu F \\
\end{align}$
Since ${{C}_{1}}^{1}>{{C}_{1}}$ ​, we can conclude that ${{C}_{1}},{{C}_{5}}$ ​ could not be connected in series. We know that series equivalent capacitance is less than each individual capacitance. Hence, ${{C}_{1}},{{C}_{5}}$ ​ are in parallel, so
$\begin{align}
  & {{C}_{1}}^{1}={{C}_{1}}+{{C}_{5}} \\
 & {{C}_{5}}={{C}_{1}}^{1}-{{C}_{1}}=1.92\mu F \\
\end{align}$

So, the correct answer is “Option B”.

Note:
The equivalent capacitance of two capacitors when connected in series will be less than the individual capacitance. Hence, in the case of capacitor one and five, we didn’t take the series case but chose the parallel setup. Hence, take care while choosing the setup as series or parallel.