Question

Let us assume that a non-conducting sphere of radius $a$ is found to be having a type charge $+q$ uniformly distributed throughout in volume. A hollow spherical conductor having inner and outer radii $b$ and $c$. The net charge $-q$ is concentric with the sphere as shown in the diagram. Read the following statements.

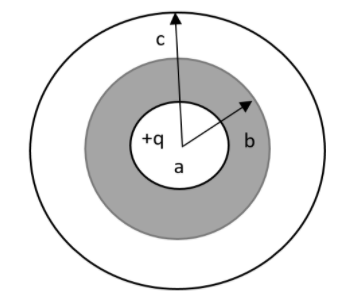
1. The electric field at a distance $r$ from the centre of the sphere $=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{qr}{{{a}^{3}}}$ for $r < a$.
2. The electric field at distance r from the centre of the sphere for $a < r < b=0$
3. The electric field at distance r from the centre of the sphere for $b < r < c=0$
4. The charge on the inner surface of the hollow sphere $=-q$
5. The charge on the outer surface of the hollow sphere $=+q$.
$\begin{align}
  & A.1,2,5 \\
 & B.1,3,4 \\
 & C.2,3,5 \\
 & D.2,3,4 \\
\end{align}$

Answer 1

Hint: The electric flux can be found by taking the ratio of the resultant charge inside the Gaussian surface to the permeability of material. This will be equivalent to the product of the electric field and the area of the wire. This all will help you in answering this question.

Complete step by step answer:
Let ${q}'$ be the inner surface of charge. Then the outer surface of charge can be found as,
${{q}_{outer}}=-q-{q}'$
The sum of the two charges can be shown as,
${{q}_{outer}}+{{q}_{inner}}=-q$
The electric field inside the conductor will be found to be zero $\left( r > b\text{ and }r < e \right)$. Therefore in the arbitrary Gaussian surface we can write that,
$\text{electric flux}=\dfrac{{{q}_{inside}}}{{{\varepsilon }_{0}}}=0$
That is written as,
$\begin{align}
  & {{q}_{inside}}\left( b < r < c \right)={q}'+q=0 \\
 & \Rightarrow {q}'=-q \\
\end{align}$
Hence from this we will get that,
$\begin{align}
  & {{q}_{inner}}=-q \\
 & {{q}_{outer}}=0 \\
\end{align}$
1. The electric field $r < a$ is given as,
$E.4\pi {{r}^{2}}=\dfrac{{{q}_{inside}}}{{{\varepsilon }_{o}}}$
As the charge is uniformly distributed,
${{q}_{inside}}=\left( \dfrac{{{r}^{3}}}{{{a}^{3}}} \right)q$
Which means that,
$E.4\pi {{r}^{2}}=\dfrac{{{r}^{3}}q}{{{a}^{3}}{{\varepsilon }_{0}}}$
$E=\dfrac{1}{4\pi }\times \dfrac{q}{{{a}^{3}}{{\varepsilon }_{0}}}$
2. For $a < r < b$, the electric field can be given as,
$E=\dfrac{kq}{{{r}^{2}}}$
3. For $b < r < c$, as we told before, $E=0$
Now the last case,
4. For $c < r$, we can write that,
$\begin{align}
  & E=\dfrac{k{{q}_{outer}}}{{{r}^{2}}} \\
 & \Rightarrow E=\dfrac{k\times 0}{{{r}^{2}}}=0 \\
\end{align}$
From this we can conclude that the 1, 3 and 4 are the correct ones.

So, the correct answer is “Option B”.

Note: A Gaussian surface is defined as a closed surface in the three-dimensional space. Through this is how we calculate the flux of a vector field. Usually the flux of the gravitational field, the electric field, or magnetic field is being measured by drawing this imaginary surface over the required surface.