Question

Let triangle ABC have vertices on a circle. Let AD be the altitude and AP be the diameter of the circle. If $\angle ABC={{84}^{\circ }}$ and $\angle BCA={{60}^{\circ }}$ then $\angle DAP $equals to \[\]

A.${{6}^{\circ }}$\[\]
B.${{12}^{\circ }}$\[\]
C.${{18}^{\circ }}$\[\]
D.${{24}^{\circ }}$\[\]

Answer 1

Hint: We join BP and CP. We use the theorem that the sum of the angles in a triangle is ${{180}^{\circ }}$ in triangles ABD, ACD to get $\angle BAD={{6}^{\circ }},\angle CAD={{30}^{\circ }}$. We use the theorem that an arc of semi-circular length always subtends right angle of measure ${{90}^{\circ }}$ to get $\angle BCP={{30}^{\circ }}$. We use the theorem that angle subtended by the same arc have equal measures to get $\angle BAP={{30}^{\circ }}$ and then we find the required angle $\angle DAP=\angle BAP-\angle BAD$.\[\]

Complete step-by-step solution
We are given in the figure a triangle ABC whose vertices are on a circle. AD is the altitude dropped on the side BC and AP is the diameter of the circle. We are further given the measure of angles $\angle ABC={{84}^{\circ }}$ and $\angle BCA={{60}^{\circ }}$. We are asked to find a measure of $\angle DAP$. Let us join BP and CP and have the figure below.\[\]

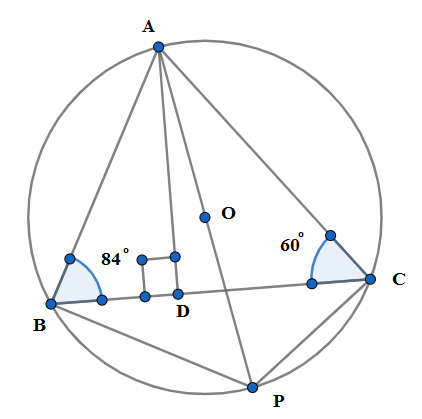
Since AD is the altitude we have $\angle ADB=\angle ADC={{90}^{\circ }}$. We know that sum of the angles in a triangle is ${{180}^{\circ }}$. So we have in triangle ADB
\[\begin{align}
  & \Rightarrow \angle ADB+\angle ABD+\angle BAD={{180}^{\circ }} \\
 & \Rightarrow {{90}^{\circ }}+\angle ABC+\angle BAD={{180}^{\circ }} \\
 & \Rightarrow {{90}^{\circ }}+{{84}^{\circ }}+\angle BAD={{180}^{\circ }}\left( \because \text{ given }\angle ABC={{84}^{\circ }} \right) \\
 & \Rightarrow {{174}^{\circ }}+\angle BAD={{180}^{\circ }} \\
 & \Rightarrow \angle BAD={{6}^{\circ }} \\
\end{align}\]
We also have in triangle ADC,
\[\begin{align}
  & \Rightarrow \angle ADC+\angle ACD+\angle CAD={{180}^{\circ }} \\
 & \Rightarrow {{90}^{\circ }}+{{60}^{\circ }}+\angle CAD={{180}^{\circ }}\left( \because \angle ACD=\angle ACB={{60}^{\circ }} \right) \\
 & \Rightarrow {{150}^{\circ }}+\angle CAD={{180}^{\circ }} \\
 & \Rightarrow \angle CAD={{30}^{\circ }} \\
\end{align}\]
We are given that AP is a diameter which means AP divides the circle into two semi-circles. We know that an arc of semi-circular length always subtends the right angle of measure${{90}^{\circ }}$ at any point on the circle. Here the semicircle has subtended $\angle ABP$ and $\angle ACP$ on the points $B,C$ on the circle respectively. So we have,
\[\Rightarrow \angle ABP=\angle ACP={{90}^{\circ }}\]
Then we have
\[\Rightarrow \angle BCP=\angle ACP-\angle ACB={{90}^{\circ }}-{{60}^{\circ }}={{30}^{\circ }}\]
We know that angles subtended by the same arc have equal measures. Here in the circle arc BP subtends angles $\angle BAP,\angle BCP$. So we have,
\[\angle BAP=\angle BCP={{30}^{\circ }}\]
Then we have
$\angle DAP=\angle BAP-\angle BAD={{30}^{\circ }}-{{6}^{\circ }}={{24}^{\circ }}$
So the correct option is D.

Note: We can alternatively solve using the sum of the angles in triangle is ${{180}^{\circ }}$ to get in triangle$\angle BAC={{36}^{\circ }}$. We then join OC and use the theorem that the central angle of an arc is twice the angle subtended on appointing on the circle but not on the arc for the arc AC to get $\angle OAC={{6}^{\circ }}$ and then the required angle $\angle DAP=\angle CAD-\angle OAC$.