Question

Let $ \operatorname{P} \left( r \right) = \dfrac{Q}{{\pi {R^4}}}r $ be the charge density distribution for a solid sphere of radius $ R $ and total charge $ Q $ . For a point $ {p_1} $ inside the sphere at distance $ {r_1} $ from the centre of sphere, the magnitude of electric field is
(A) $ 0 $
(B) $ \dfrac{Q}{{4\pi {\varepsilon _0}{r_1}^2}} $
(C) $ \dfrac{{Q{r_1}^2}}{{4\pi {\varepsilon _0}{R^4}}} $
(D) $ \dfrac{{Q{r_1}^2}}{{3\pi {\varepsilon _0}{R^4}}} $

Answer 1

Hint: To solve this question, we need to use the gauss theorem. For that we need to choose a symmetric Gaussian surface passing through the point of interest.

Formula used:
$ \Rightarrow \oint {EdS} = \dfrac{{{q_{enc}}}}{{{\varepsilon _0}}} $ , where $ E $ is the electric field, $ {q_{enc}} $ is the charge enclosed within the Gaussian surface, and $ {\varepsilon _0} $ is the electrical permittivity.

Complete step by step solution:
The sphere is shown in the below diagram.

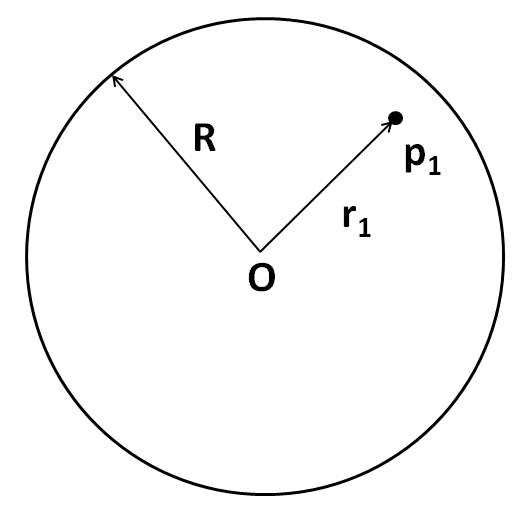
For calculating the electric field at the point p1, we use the gauss theorem which is stated as
 $ \Rightarrow \oint {EdS} = \dfrac{{{q_{enc}}}}{{{\varepsilon _0}}} $ ………………….(1)
Before using the Gauss theorem, we have to choose our Gaussian surface. We choose it to be a sphere of radius $ {r_1} $ , as shown below.

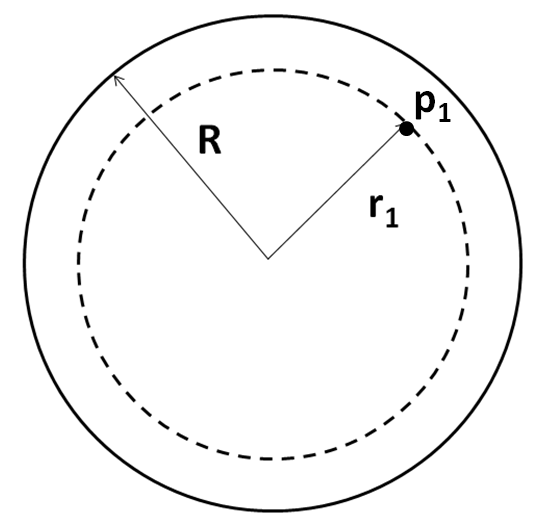
Now, we evaluate the LHS of the equation (1)
$ \Rightarrow LHS = \oint {EdS} $
As the Gaussian surface is symmetric about the charge distribution, so the electric field is constant over the whole surface. So $ E $ can be taken outside the integral
$ \Rightarrow LHS = E\oint {dS} $
$ \Rightarrow LHS = ES $
Putting the value of the surface area of the Gaussian sphere
$ \Rightarrow LHS = E\left( {4\pi {r_1}^2} \right) $
So (1) becomes
$ \Rightarrow E\left( {4\pi {r_1}^2} \right) = \dfrac{{{q_{enc}}}}{{{\varepsilon _0}}} $ …………..(2)
Now we calculate the net charge enclosed within the Gaussian surface. As the density of the sphere is non uniform, so we have to use the method of integration.

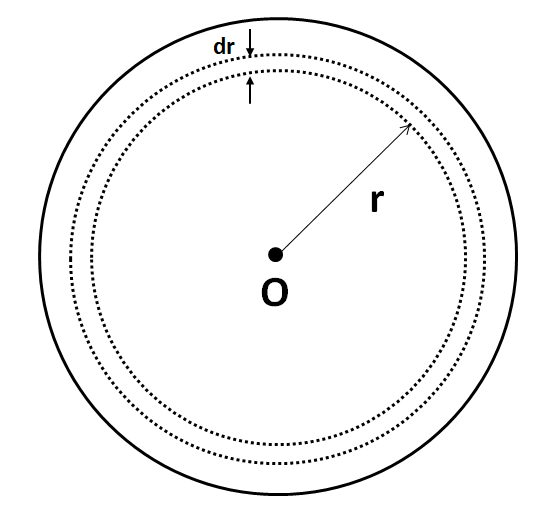
As shown in the figure, the charge on the surface of the sphere of radius $ r $ and thickness $ dr $ is
$ \Rightarrow dq = \rho dv $
$ \Rightarrow dq = \rho \left( {4\pi {r^2}dr} \right) $
According to the question, $ \rho = \dfrac{Q}{{\pi {R^4}}}r $
$ \Rightarrow dq = \dfrac{{Qr}}{{\pi {R^4}}}\left( {4\pi {r^2}} \right)dr $
$ \Rightarrow dq = \dfrac{{4Q}}{{{R^4}}}{r^3}dr $
Integrating both sides between the centre and the Gaussian surface, we get
$ \Rightarrow \int_0^{{q_{encl}}} {dq} = \dfrac{{4Q}}{{{R^4}}}\int_0^{{r_1}} {{r^3}dr} $
$ \Rightarrow \left[ q \right]_0^{{q_{enc}}} = \dfrac{{4Q}}{{{R^4}}}\left[ {\dfrac{{{r^4}}}{4}} \right]_0^{{r_1}} $
On substituting the limits we get
$ \Rightarrow \left[ {{q_{enc}} - 0} \right] = \dfrac{{4Q}}{{{R^4}}}\left[ {\dfrac{{{r_1}^4 - 0}}{4}} \right] $
$ \Rightarrow {q_{enc}} = \dfrac{{4Q}}{{{R^4}}} \times \dfrac{{{r_1}^4}}{4} $
On solving, we get
$ \Rightarrow {q_{enc}} = \dfrac{{Q{r_1}^4}}{{{R^4}}} $ ……………………..(3)
Putting (3) in (2)
$ \Rightarrow E\left( {4\pi {r_1}^2} \right) = \dfrac{{Q{r_1}^4}}{{{R^4}{\varepsilon _0}}} $
Dividing by $ {r_1}^2 $ on both the sides
$ \Rightarrow E\left( {4\pi } \right) = \dfrac{{Q{r_1}^2}}{{{R^4}{\varepsilon _0}}} $
Finally, we get the electric field as
$ \Rightarrow E = \dfrac{{Q{r_1}^2}}{{4\pi {\varepsilon _0}{R^4}}} $
Hence, the correct answer is option (C).

Note:
The choice of Gaussian surface is very much important. It should always be chosen so that it is symmetric about the charge distribution. Then only the electric field can be constant over the whole Gaussian surface, and the evaluation of the LHS of the gauss theorem will become easy.