Question

Let $K$ and $X$ represent the dielectric constant and dielectric strength of a dielectric material respectively. Which of the following properties are essential for the material to be suitable as the dielectric medium in capacitors?
A) High $K$ and high $X$
B) High $K$ and low $X$
C) Low $K$ and high $X$
D) Low $K$ and low $X$

Answer 1

Hint: Dielectric constant refers to how much the material can be polarized which leads to the reduction of the effective electric field in the capacitor. For high capacitance, the electric field must be low. Dielectric strength refers to the maximum electric field a pure material can withstand without damaging itself under ideal conditions.

Complete step by step solution:
Step 1: With the help of a diagram explain the change in capacitance on the insertion of a dielectric.

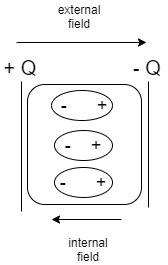
When a dielectric material is inserted between the plates of the capacitor, the dielectric material gets polarized, thus inducing an electric field ${E_{{\text{polarization}}}}$ (internal field). This electric field (external field) opposes the electric field $E$ already present in the capacitor due to its two oppositely charged conducting plates. Thus the effective electric field of the capacitor is reduced.
i.e., ${E_{{\text{effective}}}} = E - {E_{{\text{polarization}}}}$ .
The potential difference between the two plates separated by a distance $d$ is given by, $V = Ed$.
We know the capacitance of a capacitor is given by, $C = \dfrac{Q}{V} = \dfrac{Q}{{Ed}}$ . This implies that capacitance is inversely proportional to the electric field, $C \propto \dfrac{1}{E}$ .
Therefore, for high capacitance, the dielectric constant $K$ must be high.
Step 2: Explain the significance of the dielectric strength of a dielectric material.
Dielectrics are insulators or poor conductors of electricity (i.e., they have no free or loosely bound electrons). So when they are placed between the plates of the capacitors no current flows through them instead the positive and negative charges get pulled away by the external field causing the material to be polarized. As we keep on increasing the voltage (electric field), there may come a point when the dielectric suddenly becomes a conductor. This refers to a dielectric breakdown. The dielectric strength is thus a measure of the ability of the dielectric to resist a dielectric breakdown.

$\therefore $ For high capacitance, the dielectric constant $K$ must be high and must have a high dielectric strength $X$.

Note:
On introducing a dielectric the capacitance will be $C = K{C_0}$, where ${C_0}$ was the capacitance of a capacitor with a vacuum. Capacitance is inversely proportional to voltage, so as the capacitance increases on the insertion of the dielectric, the voltage decreases. This suggests that the amount of charge stored by a capacitor with a dielectric material between its plates will be the same as that stored by a capacitor without a dielectric, but it can be done at a lower voltage.