Question

Let \[f(x) = x + 2\left| {x + 1} \right| + 2\left| {x - 1} \right|\].If \[f(x) = k\] has exactly one real solution, then the value of k is
A. 3
B. 0
C. 1
D. 2

Answer 1

Hint: We use the concept of modulus and open both the terms having modulus. Divide the function into three parts on the basis of values obtained by equating both the modulus functions to zero. Calculate the value of function by substitution of values in three different parts. Plot the graph of the function using three equations formed.
* Modulus of a function ‘x’ opens up as \[\left| x \right| = \left\{ {\begin{array}{*{20}{c}}
  x&{;x \geqslant 0} \\
  { - x}&{;x < 0}
\end{array}} \right.\]

Complete step-by-step answer:
Step-by-step answer:
We are given the function\[f(x) = x + 2\left| {x + 1} \right| + 2\left| {x - 1} \right|\]
We first solve both modulus terms
(a) \[\left| {x + 1} \right|\]:
If \[(x + 1) \geqslant 0\]
\[ \Rightarrow \left| {x + 1} \right| = x + 1\]
Now we find the value of ‘x’ by equating it to zero.
\[ \Rightarrow x + 1 = 0\]
Shift 1 to RHS
\[ \Rightarrow x = - 1\]
If \[(x + 1) < 0\]
\[ \Rightarrow \left| {x + 1} \right| = - x - 1\]
Now we find the value of ‘x’ by equating it to zero.
\[ \Rightarrow - x - 1 = 0\]
Shift -1 to RHS
\[ \Rightarrow - x = 1\]
\[ \Rightarrow x = - 1\]
So, the value of x is -1.
(a)\[\left| {x - 1} \right|\]:
If \[(x - 1) \geqslant 0\]
\[ \Rightarrow \left| {x - 1} \right| = x - 1\]
Now we find the value of ‘x’ by equating it to zero.
\[ \Rightarrow x - 1 = 0\]
Shift 1 to RHS
\[ \Rightarrow x = 1\]
If \[(x - 1) < 0\]
\[ \Rightarrow \left| {x - 1} \right| = - x + 1\]
Now we find the value of ‘x’ by equating it to zero.
\[ \Rightarrow - x + 1 = 0\]
Shift 1 to RHS
\[ \Rightarrow - x = - 1\]
\[ \Rightarrow x = 1\]
So, the value of x is 1.
From (a) and (b) we have values of x as -1 and 1.
We can divide the functions into three parts \[x < 1;x \in \left[ { - 1,1} \right);x \geqslant 1\]
CASE 1: \[x < 1\]
When \[x < 1\] then \[\left| {x + 1} \right| = - x - 1;\left| {x - 1} \right| = - x + 1\]
Substitute the values in \[f(x) = x + 2\left| {x + 1} \right| + 2\left| {x - 1} \right|\]
\[ \Rightarrow f(x) = x + 2( - x - 1) + 2( - x + 1)\]
Multiply terms in the bracket
\[ \Rightarrow f(x) = x - 2x - 2 - 2x + 2\]
Add like terms
\[ \Rightarrow f(x) = - 3x\]..............… (1)
CASE 2: \[x \in \left[ { - 1,1} \right)\]
When \[x \in \left[ { - 1,1} \right)\] then \[\left| {x + 1} \right| = (x + 1);\left| {x - 1} \right| = - x + 1\]
Substitute the values in \[f(x) = x + 2\left| {x + 1} \right| + 2\left| {x - 1} \right|\]
\[ \Rightarrow f(x) = x + 2(x + 1) + 2( - x + 1)\]
Multiply terms in the bracket
\[ \Rightarrow f(x) = x + 2x + 2 - 2x + 2\]
Add like terms
\[ \Rightarrow f(x) = x + 4\]..............… (2)
CASE 3: \[x \geqslant 1\]
When \[x \geqslant 1\] then \[\left| {x + 1} \right| = x + 1;\left| {x - 1} \right| = x - 1\]
Substitute the values in \[f(x) = x + 2\left| {x + 1} \right| + 2\left| {x - 1} \right|\]
\[ \Rightarrow f(x) = x + 2(x + 1) + 2(x - 1)\]
Multiply terms in the bracket
\[ \Rightarrow f(x) = x + 2x + 2 + 2x - 2\]
Add like terms
\[ \Rightarrow f(x) = 5x\].............… (3)
We can write the function collectively as \[f(x) = \left\{
  \begin{array}{*{20}{c}}
  { - 3x}&{,x < - 1}
\end{array} \\
  \begin{array}{*{20}{c}}
  {x + 4}&{,x \in \left[ { - 1,1} \right)}
\end{array} \\
  \begin{array}{*{20}{c}}
  {5x}&{x \geqslant 1}
\end{array} \\
  \right.\]
Now we will plot the three equations (1), (2) and (3) on graph
Write \[f(x) = y\]
From \[\left( { - \infty , - 1} \right)\] we have the equation of line \[y = - 3x\]
When \[x = 1,y = - 3\]
From \[\left[ { - 1,1} \right)\] we have the equation of line \[y = x + 4\]
When \[x = - 1,y = 3\] and \[x = 1,y = 5\]
From \[\left[ {1,\infty } \right)\] we have the equation of line \[y = 5x\]
When \[x = 1,y = 5\]

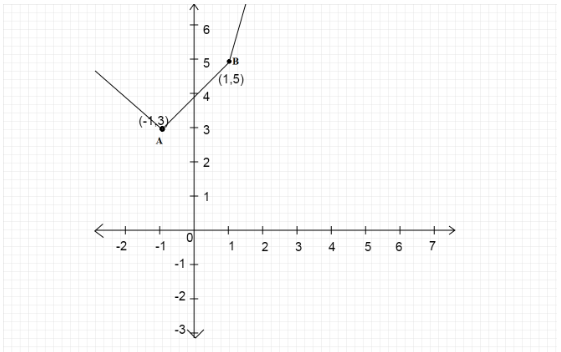
We draw a line intersecting the graph of the function at only one point.
From the figure we can see there is only one point through which we can draw a straight line that cuts the graph only at one point i.e. \[y = 3\].
Since \[f(x) = y\]
\[ \Rightarrow f(x) = 3\]
Comparing with the function \[f(x) = k\]
\[k = 3\]
\[\therefore \]Value of k is 3

\[\therefore \]Correct option is A.

Note: Students are likely to make the mistake of finding only one real solution as they confuse the word real with a positive and write solution by only looking at the positive x-axis. Keep in mind real solutions of the function means the value should be real (not complex). Also, when plotting the graph carefully, draw equations of lines to that point only till where the limit extends, many students draw lines beyond the end points.