Question

Let f be a one – one function with domain {x, y, z} and range {1, 2, 3}. It is given that exactly one of the following statements is true and the remaining two are false, \[f\left( x \right)=1,f\left( y \right)\ne 1,f\left( z \right)\ne 2\]. Determine, \[{{f}^{-1}}\left( 1 \right)\].

Answer 1

Hint: Consider the three cases one by one and check whether the given condition of one – one function is satisfied in the question or not. Eliminate the cases in which conditions are unsatisfied. Check in correct case, which of the following \[f\left( x \right),f\left( y \right)\] or \[f\left( z \right)\] has the value 1 and write the value of \[{{f}^{-1}}\left( 1 \right)\] accordingly.

Complete step-by-step solution:
We have been provided with f as a one-one function with domain {x, y, z} and range {1, 2, 3}.
We know that one – one function is a type of function in which for each value of the domain of “f” there is a particular value in the range or codomain of f.
Now, we have been provided with three statements in which exactly one is true. Let us consider three cases for this.
(i) Case (i): - When \[f\left( x \right)=1\], is true.
So, according to the question, \[f\left( y \right)\ne 1\] and \[f\left( z \right)\ne 2\] are false.
This means that \[f\left( y \right)=1\] and \[f\left( z \right)=2\] are true. Therefore,
\[\begin{align}
  & \Rightarrow f\left( x \right)=1 \\
 & \Rightarrow f\left( y \right)=1 \\
 & \Rightarrow f\left( z \right)=2 \\
\end{align}\]

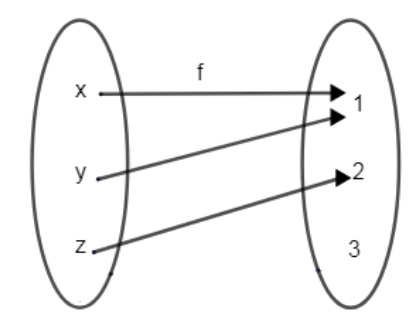
This cannot be true because the function is one – one. So, case (i) is eliminated.
(ii) Case (ii): - When \[f\left( y \right)\ne 1\] is true.
So, according to the question, \[f\left( x \right)=1\] is false and \[f\left( z \right)\ne 2\] is false. This means that \[f\left( z \right)=2\] is true. Therefore,
\[\Rightarrow f\left( y \right)=2\] or 3
\[\Rightarrow f\left( x \right)=2\] or 3
\[\Rightarrow f\left( z \right)=2\]
There is no way possible for the function to be one – one with the above situations. So, case (ii) is eliminated.
(iii) Case (iii): - When \[f\left( z \right)\ne 2\] is true.
So, according to the question, \[f\left( x \right)=1\] and \[f\left( y \right)\ne 1\] are false.
This means that \[f\left( y \right)=1\] is true. Therefore.
\[\Rightarrow f\left( y \right)=1\]
\[\Rightarrow f\left( x \right)=2\] or 3
\[\Rightarrow f\left( z \right)=1\] or 3
Here, we can form an one – one function easily by considering \[f\left( x \right)=2\] and \[f\left( z \right)=3\].

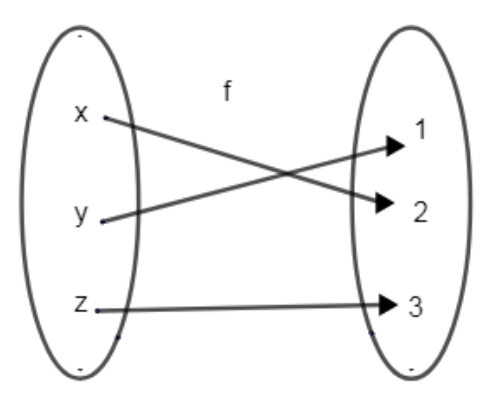
So, case (iii) is the correct case. Therefore,
\[\Rightarrow f\left( y \right)=1\]
\[\Rightarrow {{f}^{-1}}\left( 1 \right)=y\]
Hence, option (b) is the correct answer.

Note: One may note that if we will not form three cases and do not proceed accordingly then we will get confused in the three statements. The most important thing in the above question is the concept of a one-one function. So, we must remember the definition of one – one function to solve the above question.