Question

Let f : (-1, 1) $\to $ R be a function defined by f(x) = max \[\left\{ -|x|,-\sqrt{1-{{x}^{2}}} \right\}\]. If K be the set of all points at which f is not differentiable, then K will have how many values?
(a) Three elements
(b) One element
(c) Five elements
(d) Two elements

Answer 1

Hint: To solve this question we will first try to draw the graph of the function,
f(x) = max\[\left\{ -|x|,-\sqrt{1-{{x}^{2}}} \right\}\]. then we know that a function is non-differentiable at points wherever it has any sharp edges so we will then find the number of sharp edges in the graph and that will be our required value of K.

Complete step by step answer:
We have to find the number of points where function f(x) = max\[\left\{ -|x|,-\sqrt{1-{{x}^{2}}} \right\}\]. is non differentiable so for that we will first draw the graph of the given function,
Function given is,
f(x) = max\[\left\{ -|x|,-\sqrt{1-{{x}^{2}}} \right\}\]
so to draw the graph for this function we will first find out where \[-|x|\,and\,-\sqrt{1-{{x}^{2}}}\] becomes equal,
so case 1, when $-|x|=-x$, we get
\[\begin{align}
  & -x=-\sqrt{1-{{x}^{2}}} \\
 & \Rightarrow x=\sqrt{1-{{x}^{2}}} \\
\end{align}\]
Squaring both sides, we get
$\begin{align}
  & {{x}^{2}}=1-{{x}^{2}} \\
 & 2{{x}^{2}}=1 \\
 & x=\pm \dfrac{1}{\sqrt{2}} \\
\end{align}$
But only $x=\dfrac{1}{\sqrt{2}}$ is valid here because the case is when $|x|=x$, so x can’t be negative
Now, case 2 when $-|x|=x$, we get
\[x=-\sqrt{1-{{x}^{2}}}\]
Now, squaring both sides, we get
$\begin{align}
  & {{x}^{2}}=1-{{x}^{2}} \\
 & 2{{x}^{2}}=1 \\
 & x=\pm \dfrac{1}{\sqrt{2}} \\
\end{align}$
But only $x=-\dfrac{1}{\sqrt{2}}$ is valid here because the case is when$|x|=-x$, so x can’t be positive.
So we get total two values of $x$ where max function will change,
Now if we draw the graph it will look like this,

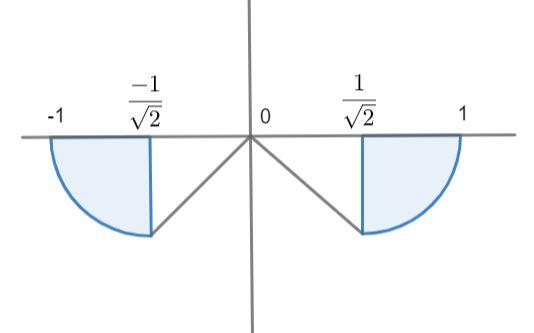
Now if we observe there are three sharp points in the graph at $x=0\,and\,x=\pm \dfrac{1}{\sqrt{2}}$, so we know the function is non-differentiable at the sharp points.
So, there will be 3 points where function will be non-differentiable, hence we get
K = $\left\{ -\dfrac{1}{\sqrt{2}},0,\dfrac{1}{\sqrt{2}} \right\}$
Hence, option (a) is correct.

Note:
While drawing the graph you need to keep in mind the points where max function changes it’s values and draw it carefully. Also in this case we are getting same values of $x$ in both the cases i.e. $x=\pm \dfrac{1}{\sqrt{2}}$ so in this question it will not matter even if you do only 1 case but you need to be careful while choosing the values of $x$ and always remember the assumption that you have taken in that particular case and choose the value of $x$ accordingly.