Question

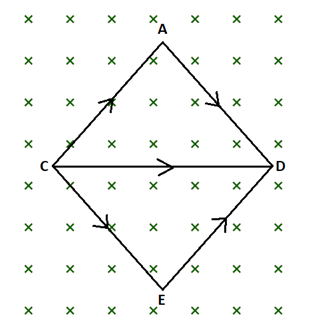
Let current $i=2A$ be flowing in each part of a wire frame as shown in figure. The frame is a combination of two equilateral triangles $ACD$ and $CDE$ of side $1\,m$. It is placed in a uniform magnetic field $B=4\,T$ acting perpendicular to the plane of frame. The magnitude of magnetic force acting on the frame is

$\begin{align}
  & A.\,\,24N \\
 & B.\,\,Zero \\
 & C.\,\,16N \\
 & D.\,\,8N \\
\end{align}$

Answer 1

Hint: From the above figure, force in both the equilateral triangles is same as the force applied in their common wire frame. For the wire frame, we can get the magnetic force acting on it using the magnetic force formula.

Formula used:
$F=IlB$, where $I$ is magnitude of current,
$l$ is length of wire, and
$B$ is the magnetic field.

Complete answer:
According to the question, it is given that:
$i=2A$, $l=1\,m$ and $B=4\,T$
From the above figure, it can be deduced that force in both the equilateral triangle is same as the force applied in their common wire frame, which can be written as:
$\overrightarrow{{{F}_{CAD}}}=\overrightarrow{{{F}_{CED}}}=\overrightarrow{{{F}_{CD}}}$
Now,
The magnitude of magnetic force acting on the frame, can be written as:
$\overrightarrow{{{F}_{net}}}=\overrightarrow{{{F}_{CAD}}}+\overrightarrow{{{F}_{CED}}}+\overrightarrow{{{F}_{CD}}}$
Since, $\overrightarrow{{{F}_{CAD}}}=\overrightarrow{{{F}_{CED}}}=\overrightarrow{{{F}_{CD}}}$ and $\overrightarrow{{{F}_{CD}}}=IlB$
Then,
$\overrightarrow{{{F}_{net}}}=(3)\overrightarrow{{{F}_{CD}}}$
$\overrightarrow{{{F}_{Net}}}=3(IlB)$
Substituting the values given in the question, we get:
$\begin{align}
  & \overrightarrow{{{F}_{Net}}}=3\times (2\times 1\times 4)\,N \\
 & \overrightarrow{{{F}_{Net}}}=(3\times 8)\,N \\
 & \overrightarrow{{{F}_{Net}}}=24\,N \\
\end{align}$

Therefore, the correct answer is Option (A).

Note:
Magnetic force acting on a frame is known by everyone. The main part in this question is getting the net force applied on the frame, once the net force is obtained then getting the answer for it is easy. Since, the given diagram shows equilateral triangle, so the net force can be equal as all the edges are of equal length.