Question

Let C be a circle and L a line on the same plane such that C and L do not intersect. Let P be a moving point such that the circle drawn with centre at P to touch L also touches C. then the locus of P is –
A. a straight line parallel to L not intersecting at C.
B. a circle concentric with C.
C. A parabola whose focus is the centre of C and whose directrix is L.
D. a parabola whose focus is the centre of C and whose directrix is a straight line parallel to L.

Answer 1

Hint: Locus is a curve or other figure formed by all the points satisfying a particular equation of the relation between coordinates, or by a point, line, or moving surface. Here as the locus P is moving then it must touch the circle C and line L at some point.

Complete step-by-step answer:
To understand the question let us draw a rough diagram by the statement given in the question

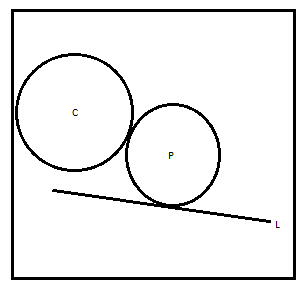
Now as we know that the locus point can move from one place to another within the same plane.
And the parabola is defined as the locus of a point which moves.
So that we can say the parabola is always at the same distance from a fixed point which we called focus and if we join the parabola and focus point we will get a line.
And when the distance between the locus and the focus is always the same then the line formed is called a directrix.
And from the question the moving point is the point P and the fixed line is the directrix and P is the focus.
So, the locus of P is a parabola whose focus is the centre C and whose directrix is a straight line parallel to L.
Hence D is the correct option.

Note: Whenever we come up with this type of problem then we must know that the locus can be a moving point or can be a stable point. It depends upon the situation that is asked in question, what condition of locus we had to take to solve the given problem.