Question

What is the length of the side BC of the given triangle? Explain how you arrived at this result?

Answer 1

Hint: To find the length of side BC, we should know the value of x because in the above figure, the length of BC is given as 4x. Now, if you carefully look at the figure then you will find that side AB and AC are equal so equate the length of AB and AC. Equating the length of AB and AC will give the value of x. And then substitute this value of x in 4x.

Complete step-by-step solution:
The figure given in the above problem is as follows:

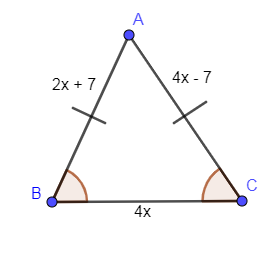
In the above figure, it is given that the sides AB and AC are equal. Also, angles B and C are highlighted this means that angles B and C are equal so when two sides and angle opposite to these sides are equal then the triangle is an isosceles triangle so equating these two sides we get,
$\Rightarrow AB=AC$
It is also given that the length of $AB=2x+7$ and $AC=4x-7$ so substituting these lengths of the sides AB and AC in the above equation we get,
$\Rightarrow 2x+7=4x-7$
Adding 7 on both the sides we get,
$\begin{align}
  & \Rightarrow 2x+7+7=4x \\
 & \Rightarrow 2x+14=4x \\
\end{align}$
Subtracting $2x$ on both the sides of the above equation we get,
$\begin{align}
  & \Rightarrow 14=4x-2x \\
 & \Rightarrow 14=2x \\
 & \Rightarrow x=7 \\
\end{align}$
From the above, we have found the value of x as 7. Now, we are asked to find the length of side BC which is given as $4x$ so substituting the value of x as 7 in $4x$ we get,
$\begin{align}
  & \Rightarrow 4\left( 7 \right) \\
 & =28 \\
\end{align}$
Hence, we have calculated the length of the side BC as 28.

Note: To solve the above problem, you should know the property that when on the sides of the triangles lines are drawn such that in the above triangle ABC, on sides AB and AC two small lines are drawn which is showing that these two sides are equal. And then taking the advantage of this property we have calculated the value of x. If we don’t know this property then we cannot solve this problem so make sure you know this property.