Question

What is the length of shortest path by which one can go from $ \left( { - 2,0} \right) $ to $ \left( {2,0} \right) $ without entering the interior of the circle, $ {x^2} + {y^2} = 1 $ :
A. $ 2\sqrt 3 $
B. $ \sqrt 3 + \dfrac{{2\pi }}{3} $
C. $ 2\sqrt 3 + \dfrac{\pi }{3} $
D.None of these

Answer 1

Hint: The perpendicular distances are always shorter than the normal distance. So, take the tangent from the point to the circle to take the perpendicular distance and also make the diagram for more clarity.

Complete step-by-step answer:
The given question when drawn on the sheet is shown below:

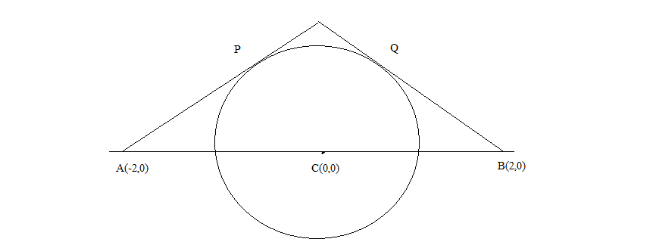
As given in the question the equation of the circle is $ {x^2} + {y^2} = 1 $ . Compare the equation of circle with general equation of circle $ {\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2} $ , where $ \left( {h,k} \right) $ is the centre of the circle and $ r $ is the radius of the circle.
After comparing it gives the centre of the circle as $ C\left( {0,0} \right) $ and the radius of the circle as $ 1 $ .
Draw the tangents from the points $ \left( { - 2,0} \right) $ and $ \left( {2,0} \right) $ to the circle $ {x^2} + {y^2} = 1 $ . It meets the circle at the points $ P\left( { - \dfrac{1}{2},\dfrac{{\sqrt 3 }}{2}} \right) $ and $ Q\left( {\dfrac{1}{2},\dfrac{{\sqrt 3 }}{2}} \right) $ .
Now the triangles $ APC $ and $ BQC $ are both right angled triangles. So, by the help of Pythagoras theorem it can be deduced that $ AP = \sqrt {C{A^2} - C{P^2}} $ and $ BQ = \sqrt {C{B^2} - C{Q^2}} $ .
The lengths $ CA $ , $ CP $ , $ CB $ and $ CQ $ can be calculated with the help of distance formula and are equal to $ 2 $ , $ 1 $ , $ 2 $ and $ 1 $ respectively.
Substitute these values we get,
 $
\Rightarrow AP = \sqrt {C{A^2} - C{P^2}} \\
   = \sqrt {{2^2} - {1^2}} \\
   = \sqrt {4 - 1} \\
   = \sqrt 3 \\
  $
And,
 $
  BQ = \sqrt {C{B^2} - C{Q^2}} \\
   = \sqrt {{2^2} - {1^2}} \\
   = \sqrt {4 - 1} \\
   = \sqrt 3 \;
  $
The arc length $ PQ $ will be equal to $ r \times \angle PCQ = 1 \times \dfrac{\pi }{3} = \dfrac{\pi }{3} $ .
The shortest distance from $ \left( { - 2,0} \right) $ to $ \left( {2,0} \right) $ is equal to sum of the lengths of $ AP $ , $ BQ $ and $ PQ $ i.e. $ \sqrt 3 + \sqrt 3 + \dfrac{\pi }{3} = 2\sqrt 3 + \dfrac{\pi }{3} $ .
So, the correct answer is “Option C”.

Note: The perpendicular distances are always shorter than any other distance and perpendicular to the boundary of the circle is always a tangent and the arc length is calculated by the angle which tangents make with each other.