Question

When the left arm of a mercury manometer is connected to a cylinder filled with a gas , the level of the mercury in the right arm rises by $2$ mm. If the pressure of the gas in the container is $110160$ Pa, the atmospheric pressure is $ \ldots \ldots \ldots \ldots $ cm of Hg. ( take $g = 10m{s^{ - 2}}$ )
A. $79$
B. $85$
C. $76$
D. $81$

Answer 1

Hint:Finding the value of atmospheric pressure, pressure of gas is balanced with atmospheric pressure and pressure due to rise in mercury manometer.

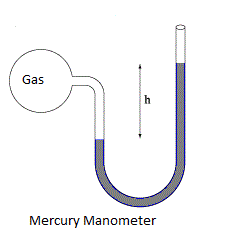
Complete step-by-step solution:Mercury Manometer left arm is attached to a gas pipe and mercury level rises by $2$ mm in the right arm as you can see in the diagram of mercury manometer.


We have pressure of gas in the container $110160$ Pa. For finding the pressure of the atmosphere, balance the pressure of the left arm with the pressure of the right arm of the mercury manometer. Let atmospheric pressure is ${P_a}$ , pressure due to rise in level of mercury in the right arm ${P_{Hg}}$ and pressure due to gas in the container ${P_G}$ .
Now, we balance the pressure of the left arm and right arm then we find that the pressure of gas is equal to atmospheric pressure and pressure due to rise in mercury level in the right arm.
$ \Rightarrow {P_G} = {P_a} + {P_{Hg}}$ $ \cdots \cdots \cdots $ equation $\left( 1 \right)$
Now, we calculate ${P_{Hg}}$ and we know that pressure is equal to the product of density, gravity acceleration and height of liquid.
$ \Rightarrow {P_{Hg}} = {\rho _{Hg}} \times g \times h$
We know that density of Mercury $\left( {{\rho _{Hg}}} \right)$ $ = 13.56$ $gc{m^{ - 3}}$ , gravity acceleration $\left( g \right) = 10m{s^{ - 2}}$ and rise in mercury level $h = 4$ mm due to fall in left arm by $2$ mm and rise in right arm by $2$mm. Put these values on above equation to get pressure of mercury,
$ \Rightarrow {P_{Hg}} = 13.56 \times 1000 \times \dfrac{4}{{10}}$ $\left( {\because 10m{s^{ - 2}} = 1000cm{s^{ - 2}}} \right)$
$ \Rightarrow {P_{Hg}} = 5424$ Pa $\left( {\because 4mm = \dfrac{4}{{10}}cm} \right)$
Now, putting value of pressure of gas ${P_G}$ , pressure due to rise in mercury ${P_{Hg}}$ in equation \[\left( 1 \right)\]
$ \Rightarrow 110160 = {P_a} + 5424$
$ \Rightarrow {P_a} = 110160 - 5424$
Now, we get
$ \Rightarrow {P_a} = 104736$ Pa
 We know that $1cm$ of Hg $ = 1333$ Pa. So, we divide the atmospheric pressure by $1333$ to get the pressure in cm of Hg.
$ \Rightarrow {P_a} = \dfrac{{104736}}{{1333}}$
$ \Rightarrow {P_a} = $$78.57 \approx 79$ cm of Hg
Hence, option $\left( A \right)$ is correct.

Note:- Pressure is also defined as force exerted in unit area. Pressure can be classified as gauge pressure, atmospheric pressure and absolute pressure.