Question

Least count of Vernier calipers is 0.01cm. When the two jaws of the instrument touch each other the 5th division of the Vernier scale coincides with a main scale division and the zero of the Vernier scale lies to the left of the zero of the main scale. Furthermore while measuring the diameter of a sphere, the zero mark of the Vernier scale lies between 2.4cm and 2.5cm and the 6th Vernier division coincides with a main scale division. Calculate the diameter of the sphere.
(a). 2.51 cm
(b). 5.12 cm
(c). 2.51 mm
(d). 5.12 mm

Answer 1

- Hint: Vernier Calipers is an equipment used to find the smallest length measurements with accuracy. According to the Vernier Calipers, actual value will be the difference between the measured value and error. Error is depending upon the Vernier calipers that we are using for the measurement. It will be different for each instrument.

Complete step-by-step solution -

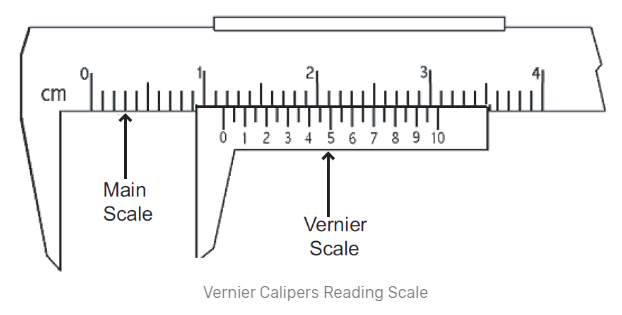
To solve the questions like this we need to go through the following steps. Here the objective is to find the true reading of the Vernier scale which would be the diameter of the sphere.

Step 1: To find the true reading of Vernier scale we can use the formula: $\text{True reading = measured reading - error}$
Now the following steps will elaborate the procedure to find measured reading and error.

Step 2: We can see that according to the question it is given that the measured reading lies between 2.4cm and 2.5cm. Here we have to use a lower scale value that is 2.4 and add the Vernier scale value to it. This will be done by the formula:
$\text{Measured reading = (lower main scale reading)+(vernier scale reading) }\!\!\times\!\!\text{ (least count)}$
We will substitute the values in the formula, we get
$\text{Measured reading}=(2.4)+6\times (0.01)$
So,
$\text{Measured reading}=2.46cm$

Step 3: As it is stated in the question that the zero of the Vernier scale lies to the left of the zero of the main scale. It means the instrument has a negative error. We can find the error by formula:
$\text{Negative error = -(vernier scale reading when two jaws are touching) }\!\!\times\!\!\text{ (least count)}$
 $\begin{align}
  & \text{Negative}\quad \text{error}=\quad -5\times 0.01 \\
 & \text{Negative}\quad \text{error}=\quad -0.05cm \\
\end{align}$
Now we have all values, so we can put the calculated values in the formula of step 1 and can get the true diameter of the sphere.
$\text{True diameter = measured reading - error}$
$\text{True diameter}=2.46-(-0.05)$
$\text{True diameter}=2.46+0.05$
$\text{True diameter}=2.51cm$
The correct option is A, that is 2.51cm.

Note: Usually students forget to add or subtract the zero error to the measured value accordingly. That results in deduction of marks. So, try to remember it. It is advised to learn the least count of Vernier Calipers. Since it determines the error of the instrument.