Question

l and m, two parallel lines, are intersected by another pair of parallel lines p and q. Show $ \vartriangle ABC \cong \,\vartriangle CDA $ .

Answer 1

Hint: In this question we will understand some basic concept of Congruent. First, we know about that in ASA (Angle Side Angle)
If any two angles and sides included between the angles of one triangle one equivalent to the Corresponding the angles and side included between the angles of the second triangle, then the triangles are said to be congruent by ASA rule.
Example-

In the above figure, $ \angle B = \angle Q,\angle C = \angle R $ and sides between $ \angle B $ and $ \angle C $ , $ \angle Q $ and $ \angle R $ are equal to each other, i.e. BC = QR. Hence, $ \Delta ABC \cong \Delta PQR $ .
Alternate angles: When two lines are crossed by another line the pair of angles an opposite sides of the transversal is called Alternate Angles.
So, students use the properties of transversal intersecting two parallel lines. i.e., interior angles are equal to each other, to show congruence of a given triangle.

Complete step-by-step answer:
In $ \vartriangle ABC \cong \,\vartriangle CDA $

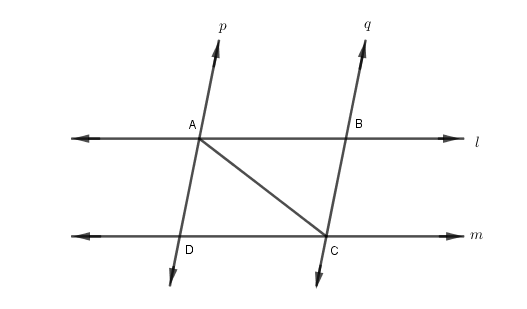
  $ \Rightarrow \angle BAC = \angle DCA $
(Since p parallel to q and AC is transversal with alternate interior angle property)
Again, $ \Rightarrow \angle BCA = \angle DAC $
Since, l parallel m and AC is transversal
Therefore, by alternate interior angle property these two angles are equal
Then, AC = AC (Common Side)
Therefore, by using A.S.A (Angle Side Angle criteria)
  $ \Delta ABC \cong \Delta CDA $ (Proved)

Note: From the above discussion we will understand the entire concept related to this question.
As we know that,
Congruent triangles are triangles having corresponding sides and angles to be equal. Congruence sides an angle to be equal. Congruence is denoted by the symbol $ \cong $ . They have the same area and the same perpendicular.
Always draw a figure to understand the situation clearly.