
Kellogg is a new cereal formed of a mixture of bran and rice that contains at least $88$ grams of protein and at least $36$ milligrams of iron. Knowing that bran contains $80$ grams of proteins and $40$ milligrams of iron per kilogram, and that rice contains $100$ grams of protein and $30$ milligrams of iron per kilogram. Find the minimum cost of producing this new cereal if bran costs ₹ $5$ per kilogram and rice costs ₹ $4$ per kilogram.
A) ₹ $4.8$
B) ₹ $4.6$
C) ₹ $3.2$
D) ₹ $4$
Answer
544.5k+ views
Hint:
For solving this particular question , we have to form equations from the given information and then try to plot the equation of lines . Find the corner points in the graph then evaluate which corner point gives the minimum cost.
Complete step by step solution:
Let the units of bran be $x$ kg , and the units of rice be $y$ kg. We know that,
We have to minimize $Z = 5x + 4y$
According to the question we have three constraints ,
$
80x + 100y \geqslant 88.......(1) \\
40x + 30y \geqslant 36........(2) \\
x,y \geqslant 0....................(3) \\
$
Now consider $80x + 100y = 88$ ,
we have , $(0,0.8)$ and $(1,0)$ .
$40x + 30y = 36$
we have , $(0,1.2)$ and $(0.9,0)$.
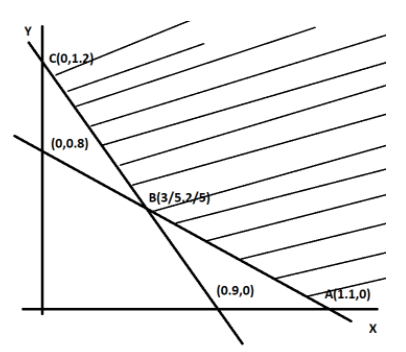
From the table it is clear that $Z$ is minimum at $B\left( {\dfrac{3}{5},\dfrac{2}{5}} \right)$
${Z_{\min }} = 4.6$
Therefore, option $B$ is the correct option.
Note:
Questions similar in nature as that of above can be approached in a similar manner and we can solve it easily. With the help of the graph, we can easily get the corner points , once we get the corner points we can find the point according to the given constraints.
For solving this particular question , we have to form equations from the given information and then try to plot the equation of lines . Find the corner points in the graph then evaluate which corner point gives the minimum cost.
Complete step by step solution:
Let the units of bran be $x$ kg , and the units of rice be $y$ kg. We know that,
| Protein | Iron | Cost | |
| Bran | 80 | 40 | 5 |
| Rice | 100 | 30 | 4 |
| Availability minimum | 88 | 36 |
We have to minimize $Z = 5x + 4y$
According to the question we have three constraints ,
$
80x + 100y \geqslant 88.......(1) \\
40x + 30y \geqslant 36........(2) \\
x,y \geqslant 0....................(3) \\
$
Now consider $80x + 100y = 88$ ,
| x | 0 | 1.1 |
| y | 22/25 | 0 |
we have , $(0,0.8)$ and $(1,0)$ .
$40x + 30y = 36$
| x | 0 | 0.9 |
| y | 1.2 | 0 |
we have , $(0,1.2)$ and $(0.9,0)$.

| Corner points | Z=5x+4y |
| A(1.1,0) | Z=5.5 |
| B(3/5,2/5) | Z=23/5=4.6 |
| C(0,1.2) | Z=4.8 |
From the table it is clear that $Z$ is minimum at $B\left( {\dfrac{3}{5},\dfrac{2}{5}} \right)$
${Z_{\min }} = 4.6$
Therefore, option $B$ is the correct option.
Note:
Questions similar in nature as that of above can be approached in a similar manner and we can solve it easily. With the help of the graph, we can easily get the corner points , once we get the corner points we can find the point according to the given constraints.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




