Question

Jupiter's period of revolution around the Sun is 12 times that of the Earth. Assuming the planetary orbits to be circular, find how many times the distance between Jupiter and the Sun exceeds that between the Earth and the Sun.
a). 5.2 times
b). 10.2 times
c). 6.4 times
d). 3 times

Answer 1

Hint: In order to solve this question, we need to use Kepler's third law that states the square of the time period of revolution of a planet about the Sun is directly proportional to the cube of the semi major axis of the orbit. And as in this case the orbit is circular, the semi-major axis will be the radius with the Sun at the center.

Complete step by step solution

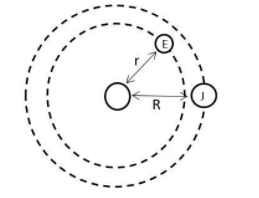
Let us assume the distance between the Sun and Earth and between Sun and Jupiter be r and R respectively. And the time period of revolution of Earth and Jupiter will be ${T}_{E}$ and ${T}_{J}$ respectively.
We know that, according to Kepler’s third law which states that the square of the time period of revolution of a planet about the Sun is directly proportional to the cube of the semi major axis of the orbit. But, according to the question, the orbit is circular in shape, so the semi major axis will be equivalent to the radius of the orbit with the Sun at the center.
Thus, we can write for Earth, ${T}_{E}^2 \propto r^3$ and for Jupiter ${T}_{J}^2 \propto R^3$.
Therefore, $\dfrac{{T}_{J}^2}{{T}_{E}^2}=\dfrac{R^3}{r^3}$,
And according to the question $\dfrac{{T}_{J}}{{T}_{E}}=12$
So, we have $\dfrac{R}{r}=12^{\dfrac{2}{3}}\implies R=5.2r$
Hence, option a is the correct answer.

Note: One other way to solve this question is by balancing the centripetal force acting on the planets and the gravitational force of attraction which will give us the velocity of the two planets. From the velocities, we can calculate the time period and then the rest is as we have already done. But the best way to solve these kinds of questions is by using the Kepler’s law.