Question

It has been mentioned that a beam of light having a wavelength $600nm$ from a distance in which the source will be falling on a single slit $1mm$ wide and causing a diffraction pattern is observed on a screen $2m$ away. Calculate the distance between the first dark fringes which will be on either side of the central bright fringe?
$\begin{align}
  & A.1.2cm \\
 & B.1.2mm \\
 & C.2.4cm \\
 & D.2.4mm \\
\end{align}$

Answer 1

Hint: The ratio of the product of the distance between the slits and the distance from the central maximum to the distance between the slit and the screen which will be equivalent to the wavelength of the light. Substitute the values in the equation. This will help you in answering the question.

Complete answer:

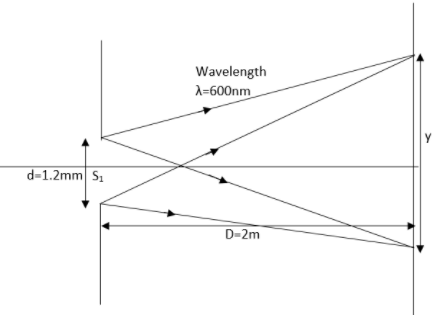
In order to produce a dark fringe the condition which is need to be satisfied will be,
The ratio of the product of the distance between the slits and the distance from the central maximum to the distance between the slit and the screen which will be equivalent to the wavelength of the light. This can be written as an equation given as,
$\dfrac{dy}{D}=\lambda $
Rearranging the equation can be written as,
$y=\dfrac{D\lambda }{d}$
The wavelength of the light which can be mentioned as,
$\lambda =600nm$
The distance between the slit has been mentioned as,
$\lambda =600nm$
The distance between the slit and the screen can be shown as,
$D=2m$
Substituting the values in this equation can be written as,
$y=\dfrac{2\times 600\times {{10}^{-9}}}{{{10}^{-3}}}=1.2mm$
Therefore the distance between the first dark fringes on either side of central bright fringe will be,
$2y=2.4mm$
Therefore the answer has been calculated.

The correct answer has been option as option D.

Note:
Diffraction which can be referred to as the different phenomena which is happening when a wave faces an obstacle or opening. It will be described as the bending of waves around the corners of a body or through a hole into the region of geometrical shadow of the aperture.