Question

Is the point \[(1,4)\] on the line represented by the equation \[x + 2y = 5\]?

Answer 1

Hint: We have to find the point \[(1,4)\] lie on the line represented by the equation \[x + 2y = 5\].
As we know that if a point lies on a line then it satisfies its equation i.e., on putting the point on the given equation we will have LHS equals to RHS. So, we will put the given point in the equation of the line and if it satisfies the equation then it lies on the given line.

Complete step-by-step answer:
We have to find whether the point \[(1,4)\] lies on the line represented by the equation \[x + 2y = 5\].
For this, we should first know that to determine if a point is on a line or not, we can simply substitute the \[x\] and \[y\] coordinates into the equation.
We have equation of line \[x + 2y = 5\], putting \[(1,4)\] in left hand side of the above equation we get
\[ \Rightarrow x + 2y = 1 + \left( {2 \times 4} \right)\]
On simplifying, we get
\[ \Rightarrow x + 2y = 1 + 8\]
On further simplification we get
\[ \Rightarrow x + 2y = 9\]
Here, we can see that on putting \[(1,4)\] in \[x + 2y\], we get \[9\]. But, for the point to lie on the line \[x + 2y = 5\], \[x + 2y\] should be equal to \[5\].
Therefore, point \[(1,4)\] does not lie on the line represented by the equation \[x + 2y = 5\].

Note: Another way to solve this problem would be to graph the line and see if it falls on the line. There are infinite numbers of lines that can pass the same given point and also there will be infinite numbers of points that will lie on the given line \[x + 2y = 5\]. We can simply substitute the \[x\] and \[y\] coordinates into the equation to check whether the point lies on the line or not.
This can be seen in the following graph

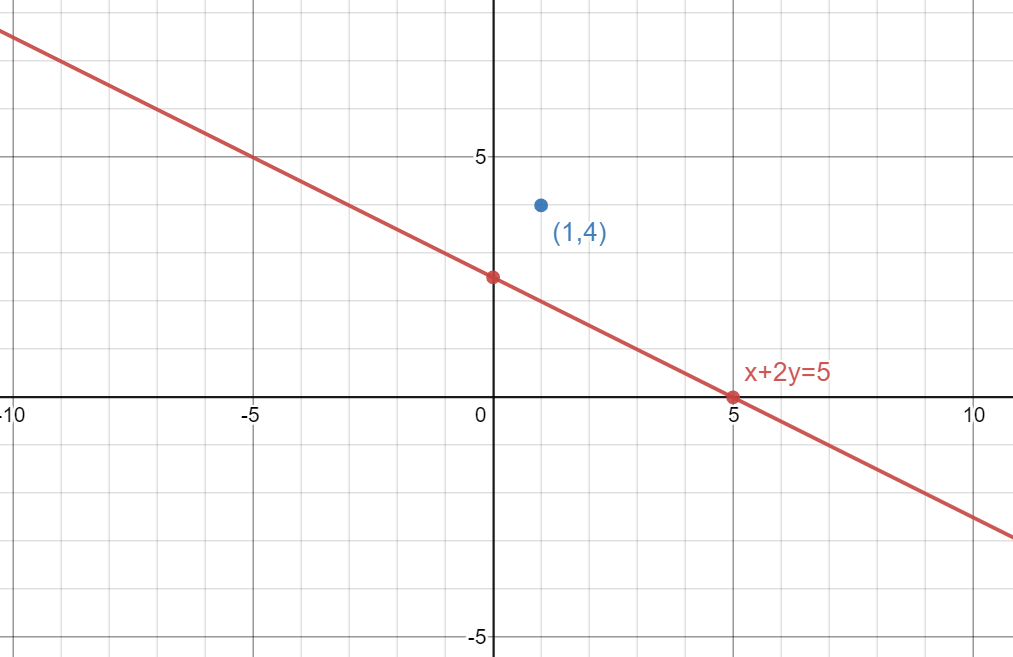
If we observe the above graph, it is clear that the point $(1,4)$ is not lying on the line $x+2y=5$.