Question

Initially, the switch is open for a long, long time. Now the switch is closed at t=0. Find the charge on the rightmost capacitor as a function of time, given that it was initially unchanged.

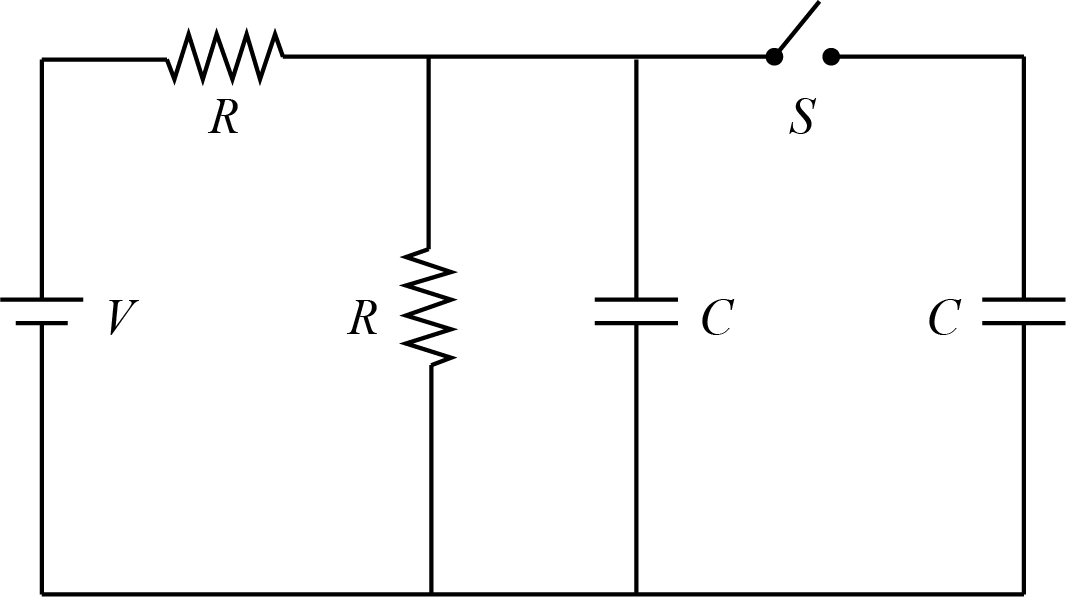
Answer 1

Hint: To solve this question, you need to use the KVL and KCL laws in the loops of the circuit, and further, you can convert the current into a differential equation of charge to solve the charge on the rightmost capacitor by integration.

Complete step by step answer:
KVL and KCL laws are very important in analyzing an electrical circuit. For the complex circuits, it gives the information of voltage and current of all nodes.
The internal circuit parameters are highly dependent on the load. In this given problem, you apply KVL and KCL to solve this circuit.

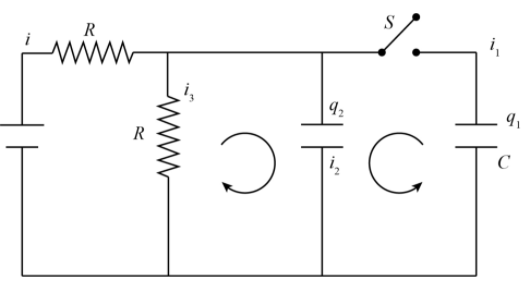
According to the KCL
$i = {i_1} + {i_2} + {i_3}$
And we know that current is the change flowing per unit time.
So, $i = \dfrac{{dq}}{{dt}}$
Since the current ${i_1}$ is going in the right-hand side capacitor, and ${i_2}$ is going in the left-hand side capacitor.
So, $\dfrac{{{q_1}}}{C} = \dfrac{{{q_2}}}{C}$
so, ${q_1} = {q_2}$
Hence the currents will also be equal, i.e., ${i_1} = {i_2}$
Applying KVL on the 2nd loop
$\dfrac{{{q_2}}}{C} - {i_3}R = 0$
Hence,
$\begin{array}{l}
\dfrac{{{q_2}}}{C} = {i_3}R\\
 \Rightarrow {i_3} = \dfrac{{{q_2}}}{{RC}}
\end{array}$
Again applying KVL on the first big loop,
$V - iR - \dfrac{{{q_2}}}{C} = 0$
Applying KCL in the bigger loop,
$\begin{array}{c}
\Rightarrow \dfrac{V}{R} = i + \dfrac{{{q_1}}}{{RC}}\\
\Rightarrow \dfrac{V}{R} = {i_1} + {i_2} + {i_3}
\end{array}$
From the above-discussed equations
$\begin{array}{c}
\dfrac{V}{{2R}} = \dfrac{{2d{q_1}}}{{dt}} + \dfrac{{2{q_1}}}{C}\\
\Rightarrow \dfrac{V}{{2R}}\int\limits_0^t {{e^{\dfrac{t}{{RC}}}}} = \int\limits_{0,0}^{q,t} {d.\left( {q,{e^{\dfrac{t}{{RC}}}}} \right)} \\
\Rightarrow \dfrac{{VC}}{2}\left( {{e^{\dfrac{t}{{RC}}}} - 1} \right) = {q_1} \cdot {e^{\dfrac{t}{{RC}}}}
\end{array}$
Hence,${q_1} = \dfrac{{VC}}{2}\left( {1 - {e^{ - \dfrac{t}{{RC}}}}} \right)$
The capacitor working is time-dependent so, in dealing with a capacitor, the time function is very important to consider. When there comes to an AC circuit, it has the prominent role of deciding the various factors dealing with the AC output. Kirchhoff's laws are the governing factor for all the AC and DC circuits. Ohm's law is based on Kirchoff's law, whether it is KCL or KVL. Ohm's law clears the relationship between the voltage and the current.
So, this is the expression of charge at t=0 for the rightmost capacitor.

Note:
We used the differential equation concept to determine the final answer. You may go wrong in solving the differential equation because the differential equation needs the understanding of calculus.