Question

In Young's double slit experiment the distance of the nth dark fringe from the centre is:
(A) $n\left( {\dfrac{{\lambda D}}{{2d}}} \right)$
(B) $n\left( {\dfrac{{2D}}{{\lambda d}}} \right)$
(C) $\left( {2n - 1} \right)\left( {\dfrac{{\lambda D}}{{2d}}} \right)$
(D) $\left( {n - 1} \right)\left( {\dfrac{{4D}}{{\lambda d}}} \right)$

Answer 1

Hint: First, we can explain the structural set up of Young’s double slit experiment. Then, using the condition to obtain a dark fringe, we can find the solution.

Complete step by step answer:Let us consider the diagram below showing Young’s double slit experiment. Let ${S_1}$ and ${S_2}$ are the slits through which the monochromatic light of wavelength$\lambda $ is passed. Let $d$ be the distance between the slits and $D$ be the distance from the plane of the slits to the screen where the fringes are formed. We can take $y$ as the distance from the centre $O$ of the screen to the point $P$. Consider that the light waves coming out of the slits ${S_1}$ and ${S_2}$ interfere destructively at the point $P$. A dark fringe is formed when there is a destructive interference of the waves. We assume that the ${n^{th}}$ dark fringe is formed at the point $P$.

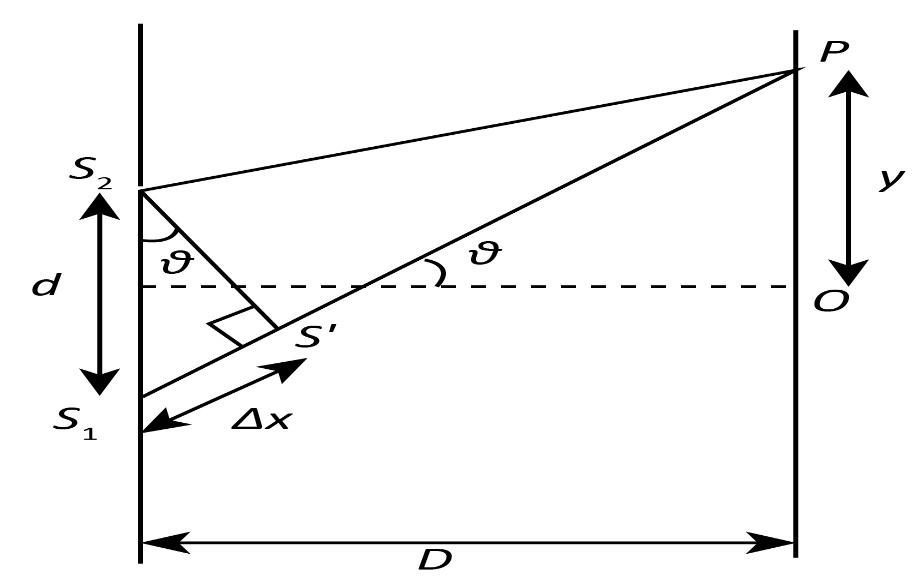
Now, the path difference of the waves can be written as

$\Delta x = {S_2}P - {S_1}P$

From the , we get

$\sin \theta = \dfrac{{\Delta x}}{d}$

Here $\theta $ is the angular position of the ${n^{th}}$ dark fringe.

Hence, we can write

$\Delta x = d\sin \theta $

Again, from the figure, we can write

$\sin \theta = \dfrac{y}{D}$

We can substitute $\dfrac{y}{D}$ for $\sin \theta $ in the equation $\Delta x = d\sin \theta $. Then,

$\begin{array}{c}
\Delta x = \dfrac{{dy}}{D}\\
\Rightarrow y = \dfrac{{\Delta xD}}{d}
\end{array}$

In Young’s double slit experiment, the condition to obtain a dark fringe can be written as

$\Delta x = \left( {2n - 1} \right)\dfrac{\lambda }{2}$

Now, we can use this condition in the equation $y = \dfrac{{\Delta xD}}{d}$. Therefore, we get

$y = \left( {2n - 1} \right)\dfrac{\lambda }{2}\dfrac{D}{d}$

So, the distance of the ${n^{th}}$ dark fringe from the centre is $\left( {2n - 1} \right)\dfrac{\lambda }{2}\dfrac{D}{d}$. Therefore, the option.

Note:We can get confused with the conditions for obtaining a bright fringe and a dark fringe. For obtaining a bright fringe, the path difference should be an integer multiple of the wavelength of light.