Question

In Young’s double slit experiment fringe order is represented by ‘m’ then fringe width is –
A) Independent of m
B) Directly proportional to m
C) Directly proportional to \[(2m+1)\]
D) Inversely proportional to \[(2m+1)\]

Answer 1

Hint: We can find the relation between the fringe width and the fringes, if any, by substituting the equation of the distance of each fringe from the origin of O. By finding the difference between two such distances will give us the fringe width in interference pattern.

Complete answer:
 Let us consider a Young’s double slit experiment. Let there be a monochromatic source of light with wavelength \[\lambda \], which is placed equidistant from the two slits with slit width ‘d’ (AS and BS) as shown in the figure below.

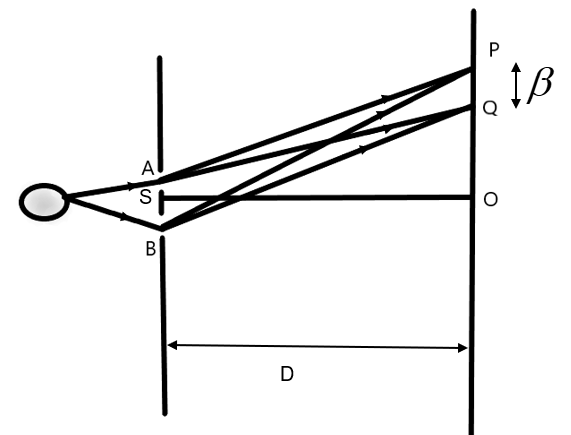
We can assume from the figure that the points P and Q on the screen at a distance of ‘D’ are two consecutive points of constructive interference. The fringe width (\[\beta \]) is the distance between two consecutive constructive or destructive interferences.
We know the formula to find the distance from O to P and O to Q as –
\[{{x}_{n}}=\dfrac{m\lambda D}{d}\]
Where m is the fringe order.
Let us find the distance from O to the consecutive constructive interference points P and Q –
\[\begin{align}
  & OP={{x}_{m+1}}=\dfrac{(m+1)\lambda D}{d} \\
 & \text{and,} \\
 & OQ={{x}_{m}}=\dfrac{m\lambda D}{d} \\
\end{align}\]
Now, we can find the fringe width easily by find the difference between OP and OQ as –
\[\begin{align}
  & \beta =OP-OQ \\
 & \Rightarrow \text{ }\beta ={{x}_{m+1}}-{{x}_{m}} \\
 & \Rightarrow \text{ }\beta =\dfrac{(m+1)\lambda D}{d}-\dfrac{m\lambda D}{d} \\
 & \therefore \text{ }\beta =\dfrac{\lambda D}{d} \\
\end{align}\]
From the above the equation of fringe width, we understand that it is independent of the fringe order. Therefore, in an interference pattern, the fringe order is a constant.

So, the correct answer is “Option A”.

Note:
We should not get confused with the fringe width in interference and diffraction. The Young’s double slit experiment is an interference phenomenon and therefore, the fringe width is always constant for a given setup. This is not true for a diffraction.