Question

In YDSE with monochromatic light, fringes are obtained on the screen placed at some distance from the slits. If the screen is moved by $5\times {{10}^{-2}}m$ towards the slits, fringe width changes by $3\times {{10}^{-5}}m$. If separation between the slits is ${{10}^{-3}}m$ and wavelength of light used is $\mathring{A}$, then what is the magnitude of $y$?
(Assume distance between the two slits is very small than the distance between the slits and screen)

Answer 1

Hint: Use fringe width formula for Young’s Double Slit Experiment to obtain wavelength of incident light. The wavelength of light used is given in terms of $y$. Use the given relation to obtain its magnitude.

Formula used:
Fringe width, $\beta =\dfrac{\lambda D}{d}$

Complete step by step answer:
In Young’s Double Slit Experiment, the fringe width obtained on the screen depends on wavelength of incident light, distance between screen and slits and distance between the slits as
$\beta =\dfrac{\lambda D}{d}$
Where $\lambda$ is the wavelength, $d$ is the distance between the slits and $D$ is the distance between the screen and the slits.

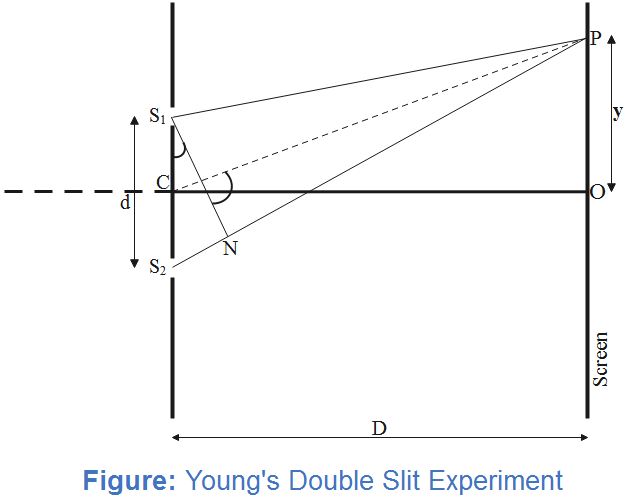
When the screen is moved by $5\times {{10}^{-2}}m$ towards the slits $D$ decreases by this magnitude.
Change in fringe width can be written as
$\Delta \beta =\left| \dfrac{\lambda {{D}_{2}}}{d}-\dfrac{\lambda {{D}_{1}}}{d} \right|$
Substituting the corresponding values, we are given the change in fringe width as $3\times {{10}^{-5}}m$ when screen is moved by $5\times {{10}^{-2}}m$ towards the slits
$3\times {{10}^{-5}}\,m=\dfrac{\lambda }{d}\left( {{D}_{2}}-{{D}_{1}} \right)=\dfrac{\lambda }{{{10}^{-3}}m}\left( 5\times {{10}^{-2}} \right)$
On rearranging the equation and solving, we get
$\lambda =\dfrac{3}{50}\times {{10}^{-5}}m=6000{\mathring{A}}$
Since wavelength of light is given as $1000y{\mathring{A}}$, we can write
$1000y=6000$
This implies that $y=6$
Hence, it can be concluded that the magnitude of $y$ is 6.

Additional Information:
When waves from two coherent sources superimpose, interference occurs. Where both waves interfere constructively, bright fringe is observed and where the waves interfere destructively the fringe obtained is dark. Interference will be constructive or destructive depending on the path difference between the waves.

Note:
Fringe width is the distance between two consecutive minima or two consecutive maxima in YDSE. Fringe width depends on wavelength of incident light, distance between screen and slits and distance between the slits.
Students must remember relation for fringe width as questions related to fringe width are often asked in exams.