Question

In what ratio must rice be at Rs. 9.30 per kg mixed with rice at Rs. 10.80 per kg so that the mixture be worth Rs. 10 per kg?
(a) 7:8
(b) 6:7
(c) 7:6
(d) 8:7

Answer 1

Hint: Here, we will assume the required ratio to be x:y. It means x kg of the rice whose price is Rs 9.3 per kg is taken and y kg of the rice whose price is Rs 10.8 per kg is taken. We will then use the condition given in the question to find the value of x:y.

Complete step-by-step solution -
The allegation corresponding to this is given below:

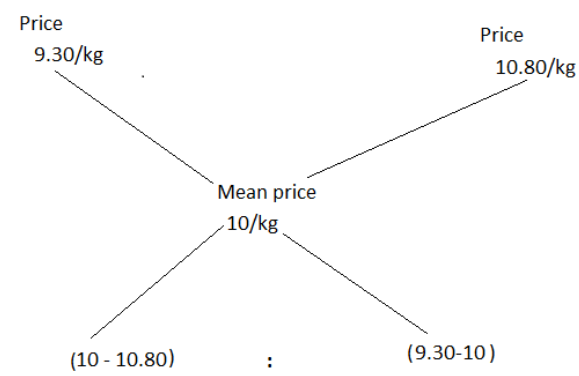
The numbers in a ratio may be quantities of any kind, such as counts of people or objects, or such as measurements of lengths, weights, time, etc. In most contexts, both numbers are restricted to be positive. A ratio may be specified either by giving both constituting numbers, written as "a to b" or a∶b, or by giving just the value of their quotient $\dfrac{a}{b}$ . Equal quotients correspond to equal ratios.
Consequently, a ratio may be considered as an ordered pair of numbers, as a fraction with the first number in the numerator and the second as denominator, or as the value denoted by this fraction. Ratios of counts, given by (non-zero) natural numbers, are rational numbers, and may sometimes be natural numbers. When two quantities are measured with the same unit, as is often the case, their ratio is a dimensionless number. A quotient of two quantities that are measured with different units is called a rate.
Let us consider that the x kg of the rice having price Rs 9.3 per kg is taken, then we can say that:
Since the price of 1 kg rice is Rs 9.3.
So, price of x kg rice is = $Rs9.3\times x$
Again consider that y kg of rice having price Rs. 10.80 per kg is taken, then we can write:
Since, price of 1 kg rice is = Rs. 10.80
So, price of y kg rice is = $Rs10.80\times y$
Total cost of rice = $Rs9.3x+Rs10.80y$
Total amount of rice = x + y
So, price of 1 kg rice after mixing them = $\dfrac{Rs\left( 9.3x+10.8y \right)}{\left( x+y \right)}$
Since, it is given that the price of 1 kg rice after mixing is Rs. 10.
So, $\dfrac{\left( 9.3x+10.8y \right)}{\left( x+y \right)}=10$
$\begin{align}
  & \Rightarrow 9.3x+10.8y=10\left( x+y \right) \\
 & \Rightarrow 10.8y-10y=10x-9.3x \\
 & \Rightarrow 0.8y=0.7x \\
 & \Rightarrow \dfrac{x}{y}=\dfrac{0.8}{0.7}=\dfrac{8}{7} \\
\end{align}$
So, x:y = 8:7.
Hence, option (d) is the correct answer.

Note: Students should note here that Rs. 10 is the price of 1 kg rice after mixing both kinds of rice. So, we have to divide the total price by the total quantity of rice. The calculations must be done correctly and the mixture allegation diagram must be drawn properly.